擬似位相整合は、非線形相互作用、特に、非線形周波数変換の際の位相整合と同じような結果を実現する手法である。均質な非線形結晶材料の代わりに、空間的に変調された非線形性質が用いられる。考え方としては、本質的に、ある伝搬距離にわたって位相の不整合性を許すことであるが、間違った変換方向に相互作用がおこる可能性のある場所において非線形相互作用を反転 (あるいは、阻害) することである。複屈折位相整合と対照的に、波が異なった偏向状態である必要がない。事実、同じ偏向状態を持つことはあまり珍しくはない。 (専門用語としては、 “type-0 位相整合” が使われる。)
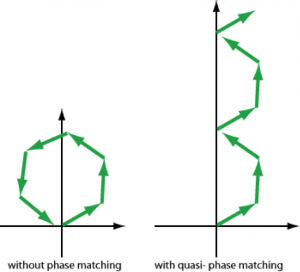
図 1: 結晶の異なる場所からの振幅の寄与の和。擬似位相整合をすることで、高変換効率が実現できる。
図1は、周波数二倍器内における高調波に対する、非線形結晶の異なる場所からの複素振幅の寄与を緑の矢印で示している。位相整合がない場合は、これらの寄与は、結晶内のかなりの距離にわたって建設的に足されることはない。擬似整合を用いると、それぞれの寄与が全振幅を消すような場所で、寄与の向きを反転させる。(いわゆるコヒーレント長を超える伝搬後に当てはまる場合である。) そのようにして、本当の位相整合ほど素早くはないものの、振幅の総和は、どんどん大きくなっていく。
完璧に位相整合された場合と比較して、もし、非線形係数が同じである場合、擬似位相整合では、変換効率が小さくなる。実効非線形係数 deffは、2 / πのファクターで減衰する。しかし、擬似位相整合を用いると、すべての相互作用する波に対して同じ偏光方向を用いることができ、これによって、しばしば、非線形テンソルのより大きな素子を用いることができる。事実上、変換効率は、本当の位相整合よりもかなり大きくなることがある。例として、複屈折位相整合において通常、係数d31 = 4.35 pm/Vを使用している、ニオブ酸リチウム (LiNbO3) を考えてみる。その一方で、擬似位相整合では、通常より大きな係数d33 = 27 pm/Vを用いているが、結果として、上記に述べた係数である2 / πを考慮すると17 pm/Vとなる。通常、変換効率は、非線形係数の二乗に比例する (低変換領域では) ので、d33を用いた結果、励起パワーが制限される等の理由であまり高い光強度が用いられない場合において、非常に大きな利点となっている。擬似位相整合は、現在、周波数二倍化 (例、緑および青のレーザー光源) や光パラメトリック発振器のようなパラメトリックデバイスに広く用いられている。
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。