第４章　1. レーザーマクロ加工の種類と基礎現象

1. レーザーマクロ加工の種類と特長

レーザーを熱源とするマクロ材料加工は、大別して、1）物質除去加工、2）接合加工、3）表面改質加工、および4）その他の加工、に分類される。それぞれの加工は更に細分化されて、多くの加工法が提案されている。表1に代表的なレーザーマクロ加工法をまとめて示す。
これらの加工法のうち代表的なものについては、次節以降に詳細に述べる。
レーザー加工の一般的特長は、

• 非接触加工
• 高速加工
• 咼品質加工
• 高精度加工
• 低歪・低変形加工

である。これは、レーザービームが小さなスポット径に集光出来るため、加工が微少領域で極短時間に完了するため、熱加工でありながら熱影響が非加工物の広い範囲に及ばないためである。

目次へ ∧

2. 金属による光吸収の理論

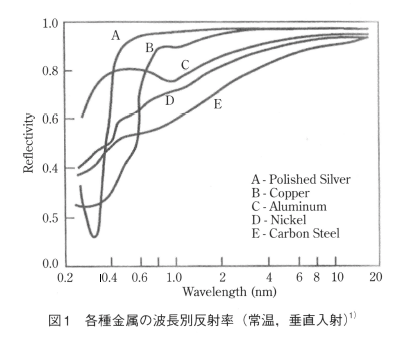
レーザー熱加工は、集光したレーザービームを非加工物に照射し、照射部近傍に材料の熱的変化を生じさせる加工法である。現在、レーザー加工が最も多く適用されているのは金属材料である。しかし、一般に金属は光の良い反射体である。図1に幾つかの金属平面の反射率と波長との関係を示す。
図1から明らかな様に、金属材料は長波長の光に対して高い反射率を有する。産業界で最も広く利用されているレーザーは赤外域の炭酸ガスレーザー（波長:10.6μm）とNd:YAGレーザー（波長:1.06μm）であるが、何れのレーザーの波長も金属によって強く反射される。これはレーザー照射部の加熱が生じにくい事を意味し、このためレーザー加工では加熱のためのフォトンコストが非常に高くなる問題点がある。
固体中での電磁波の伝播速度と減衰、すなわち分散は電磁波の振動数により異なり、分散のメカニズムは大きく分けて 1）双極子（束縛電子）によるもの、2）自由電子によるもの、及び 3）不純物や欠陥によるもの、等がある。金属の場合は主として 2）を考えればよいが、金属内の電子はガス体のプラズマと異なってバンド構造を有すること及びボルツマン分布ではなくフェルミ分布を呈することなどの理由により光の分散あるいは吸収のメカニズムはプラズマガスあるいは電子ガス（ローレンツガス）に比べて遥かに複雑である。しかし、金属導体の場合には電子が吸収のメカニズムに深く関与している点では先述のプラズマ又はローレンツガスの場合と類似している。
導電固体中の電子による吸収を考える場合、光の電界により加速された電子が結晶格子と衝突により誘起される格子振動（フォノン）や電子同士の衝突等を考慮せねばならない。Drude^2）は1900年に光の金属中自由電子による吸収理論を初めて提唱した。これらの理論の詳細については、例えば、Prokhorovら³⁾により詳細に解説されている。
衝突を特徴付ける物理量に衝突時間τあるいは衝突周波数Γがあり、これらは次の関係で結ばれている。

ここで、衝突周波数Γは電子-フォノン衝突周波数Γ_ep、電子-電子衝突周波数Γ_ee、電子-不純物（又は欠陥）衝突周波数Γ_ed、等の和として表わされる。すなわち、

金属内に垂直入射する平面波（電界方向:χ）による電子の運動は次の様に記述出来る。

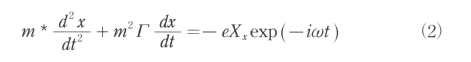
ここにm*は金属内における電子の実行質量で、電子の質量をm、束縛電子密度をn₀、自由電子密度をn_eとすると次の様に定義される。

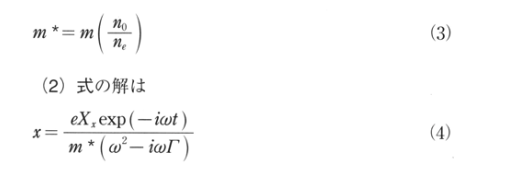
解（4）から金属の導電率σや入射平面波の金属内における偏光度α_p等が導出できる。

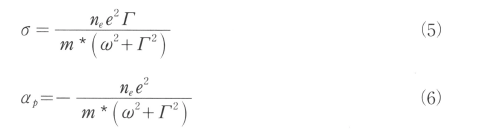
（5）及び（6）式においてω=0とおけば直流導電率及び直流偏光度となる。

金属の複素誘電率ε_cは次の様に書け、（5）及び（6）を用いると次式が得られる。

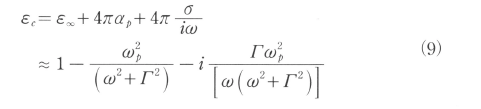
ここでω→∞でε（∞）→1となることを考慮している。またω_pは次式で示される金属内自由電子のプラズマ振動数である。

常温における金属内のプラズマ角周波数の大きさはω_p〜10¹⁶rad/s程度である。
複素誘電率は通常次の様に書く。

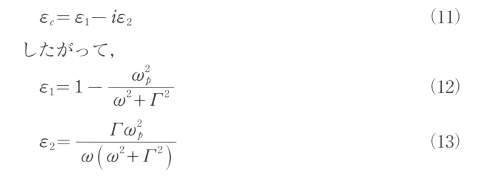
垂直入射光に対する金属の光学定数、即ち複素屈折率n_cと反射率R_Dは（12）及び（13）の関係式を用いて次のFresnelの公式が得られる。

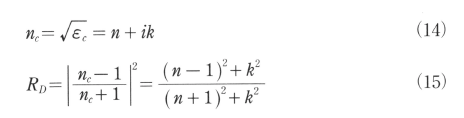
ここに、nは屈折率、kは減衰定数であり、ε₁とε₂との間に次の関係が成立する。

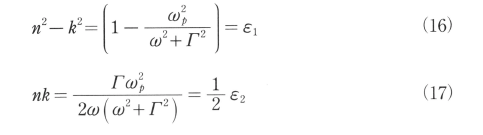
上記の関係および式（7）から、金属の電気特性と光学特性との関係を関係づける古典的なDrudeの理論が得られる。（16）、（17）式から屈折率n及び減衰定数おは次の様になる。

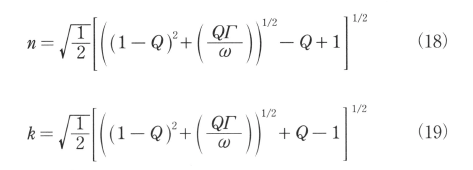
ここに、

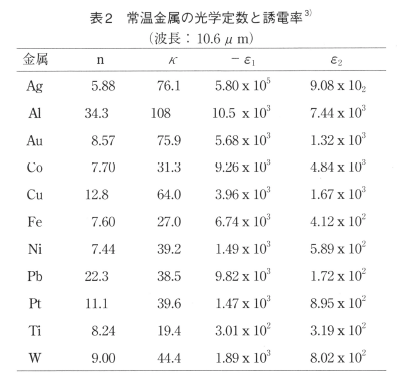
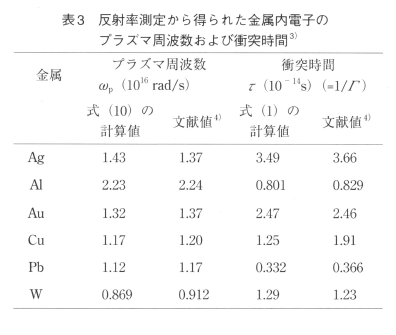
表2に炭酸ガスレーザーの波長（10.6μm）に対する代表的な純金属の光学定数n及びκと誘電率ω₁及びω₂を示す。また表3にプラズマ振動数ω_p及び衝突時間τの値を示す。
さて、nとkが計算出来れば（11）式から表面反射率R_D及び吸収率力AD（=1-R_D）の波長依存性が計算出来ることになる。しかしこのためには（20）式におけるω_pとΓが既知でなければならない。しかし、これらの物理量は特に合金において分っておらず、また推定の方法も確立されていない。そこで、通常は（18）、（19）及び（15）式をω_pに対するωとΓの大きさによって近似化し、あとは測定結果から修正する方法がとられる。以下に、近似化の例を示す。

Ⅰ）ω_p²>>ω²>>Γ²の場合：AgやAu等の純金属の場合
式（15）、（18）および（19）より次の関係が得られる。

Ⅱ）ω_p²>>ω²〜Γ²の場合：AlやCu等の場合
この場合は単純な解析解で近似式を表示することは出来ない。しかし、種々の仮定のもとn>1、k>1の場合には次の近似式が提唱されている。

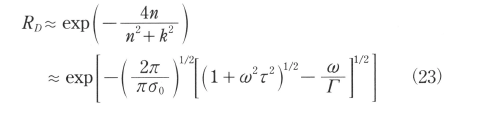
ここに、σ₀は直流導電率である。金属では表２に見るようにn>>1、k>>1であるから、上式は十分な精度で使用できる。

Ⅲ）ω_p²>>ω²、n²+k²+2n>>1の場合：
WoostenあるいはKonov等によって次の近似式が提唱されている。

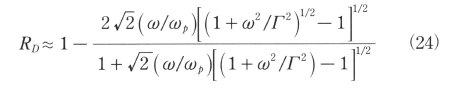
上式において、炭酸ガスレーザーの波長（10.6μm）に対して分子が非常に小さくなる金属に対しては（24）式は次の様に簡素化される。

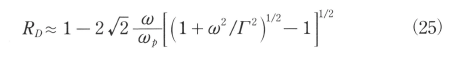
以上述べたDrudeモデルにおける光の吸収される浸透深さδ_Dは次式の様になる。

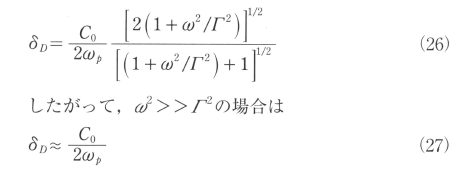
となる。
Drudeモデルの適用範囲は電子の慣性が入射光の振動に追随できる場合である。したがって、長波長の光、すなわち振動数の低い赤外光に対してモデルは比較的良く一致する。
古典論では吸収係数力りは（22）式で表わされた。しかし電子のバンド間遷移を伴う場合は衝突時間又は衝突周波数は古典論のそれと異なるので実効的な値を用いなければならない。したがって（1）及び（22）式は表示上次の様に書き換えられる。

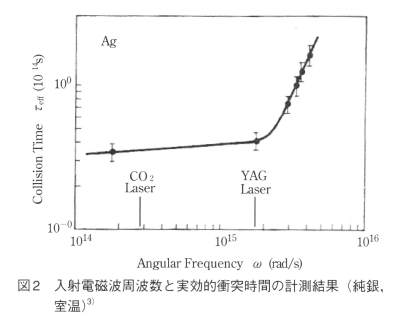
しかし、現在Γ_effがを理論的に計算できる段階に至っていないので実験的にA_effかを決定し、その結果からΓ_effがを評価しなければならない。このバンド間遷移に伴う補正は、実験的に求められた入射電磁波の限界波長入Bまたは限界角周波数0IBを観測することにより行われる。図2は室温の純銀の異なる振動数（波長）における光吸収測定から求められた衝突時間可の変化を示す。τ_effが急激に増加する周波数域（波長域）ではバンド間遷移が顕著になる領域である。
図2の場合λ>1μmでは古典論が適用できるが、λ<1μmではバンド間遷移を考える必要がある事を示している。この限界波長入Bは当然材料により異なり、純アルミニウムの場合にはYAGレーザー波長（1.06μm）に対しては古典論により与えられる吸収係数はA_D〜1.1×10^-2となるが、バンド間遷移を考慮するとA_IB〜4.5×10^-2となり、吸収率は古典論の4倍となる事が明らかにされている。
表3に幾つかの純金属に対する金属内電子のプラズマ振動数及び衝突時間の計算値及び近赤外及び12μmまでの波長域における計測結果を示す。

目次へ ∧

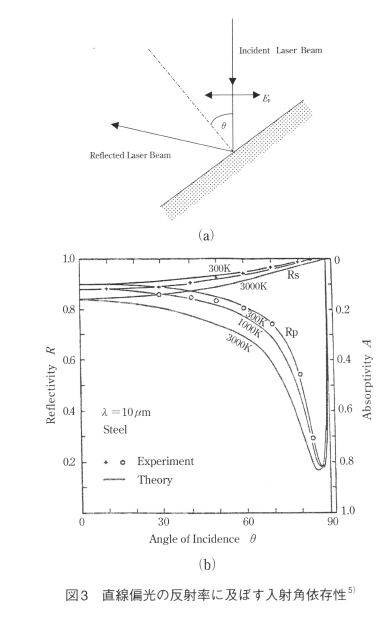
3. 斜め入射光の反射と吸収

垂直入射では光の偏光は反射及び吸収に何の影響も与えないが、斜め入射の場合は直線偏光の方向と入射面の方向により反射・吸収特性が異なる。いま図3（a）に示すような入射光の偏光方向と表面の位置関係にあるときの反射率は入射角度により図3（b）のように変化する事が知られている⁵⁾。すなわち直線偏光の方向（p一波）に面を傾けると角度増加と共に反射率は次第に減少し、90°近くの角度（Erewster角と呼ぶ）で最小となった後90°で全反射される。一方直線偏光の方向と直角（s一波）の方向に面を傾けた場合は反射率は単調に増加し、90°で全反射する。なお、通常の材料加工用レーザーは円偏光となるように調整されており、この場合の反射率の角度依存性は直線偏光のs一波と同じ挙動を示す。
いまn²+k²>>1が成立する場合、p-波及びs一波の反射率はFresnelの公式により次の様に表わされる。

なおここで注意すべき事は、斜め照射の場合は照射部面積S_Sが角度増大と共に大きくなりS_S〜l/cosθとなるため入射強度は1/cosθだけ減少する。

目次へ ∧

4.吸収率の温度依存性

金属表面に於ける光の吸収は温度と共に変化する。金属のレーザー表面改質ではレーザー照射により溶融点近傍もしくはそれ以上に急速に加熱する場合が多い。そこで温度変化に伴う光の吸収について若干述べる。実用的なレーザー表面改質に用いるレーザー波長範囲では前述の様にDrudeの理論が比較的良く適用できるのでここではその観点から説明する。
前述したように、ω_p²>>ω²>>Γ²では吸収率は（22）式の様になる。

この式に（7）式で示した直流導電率を代入すると、

が得られる。すなわち、導電率の高い金属ほど吸収率が低くなる。全ての金属は温度上昇と共に導電率が低くなる事は良く知られている。したがって、（38）式より高温では光の吸収率は増加する事が定性的に理解できる。
一般に常温の純金属については吸収率はかなり良い精度で測定も計算も可能になっている。そこで高温での吸収率を推定するために次の手法がとられる。すなわち、

または、より一般的に

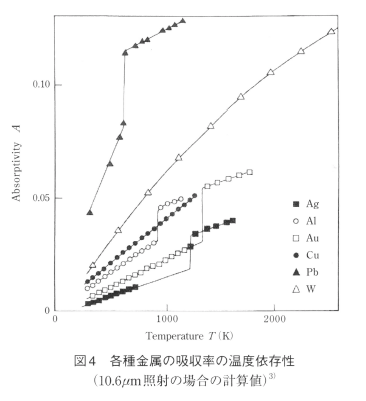
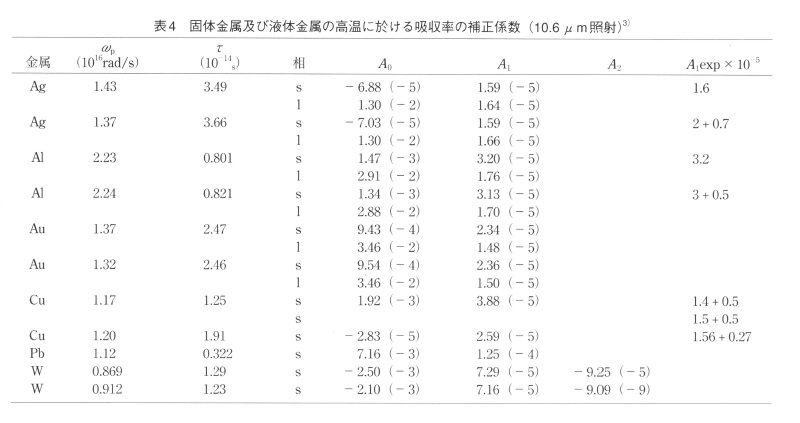
表4にCO₂レーザー波長に対する幾つかの超高純度金属に関する上式の係数んをプラズマ周波数及び衝突時間の値と共に示す。
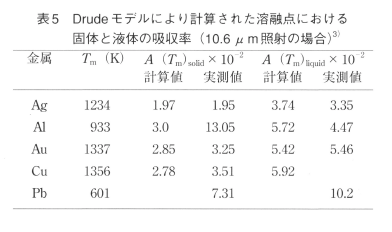
溶融が生じると、自由電子密度の減少及び金属原子の密度低下が不連続的に生じるため、光の吸収率は不連続的に増加する。表5はこれらの事を考慮した上でDrudeモデルにより計算した溶融点に於ける固体及び液体状態でのCO₂レーザー波長の吸収率を示す。液体になると吸収率は不連続的に上昇し、その大きさは固体の場合の1.5〜2倍程度となる。また図4はこの様にして計算した吸収率の温度依存性を示す。
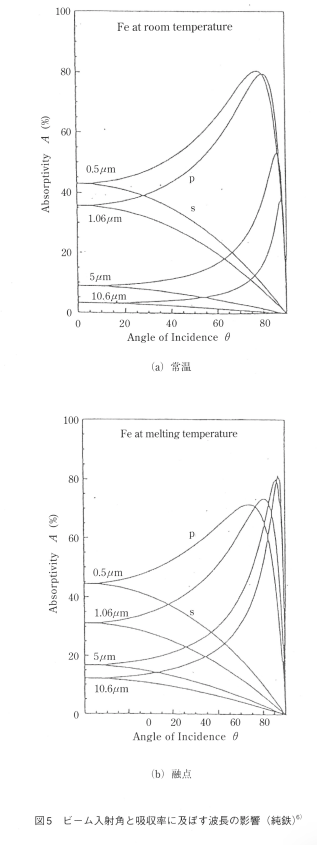
以上の様に長波長の光吸収についてはDrudeモデルの計算値と実測値は比較的良い精度で一致するが、短波長レーザー、例えばYAGレーザーに対しては古典的なDnideモデルでは計算の精度が必ずしも良くない。短波長レーザービームの高温に於ける吸収率の計算は前述したバンド間遷移を考慮したモデルを用いると精度は大いに改善されるが、ここではその説明の詳細は割愛する。図5はこの様にして計算された純鉄におけるビーム入射角と吸収率に及ぼす波長の関係を常温と溶融点の場合について示す。常温の場合、p一波で最大吸収が生じる入射角は波長が短くなるにつれ低角度側へ移行するとともに、吸収率は増加する。一方、溶融状態においては、長波長ほど吸収率が著しく増加し、常温の場合と逆転が生じる。
以上の理論計算による吸収率の決定は純金属については非常に改善されているが、合金については合金成分が非常に少ない場合を除いては計算が困難である。したがって、実用合金については未だ実測に頼らざるを得ない場合が多い。また、実用材料の殆どは表面に酸化物等が存在したり表面が鏡面でないため、必ずしも理論値が適用できるとは限らない。特にアルミニウム合金の場合には表面酸化物皮膜の形態及び厚さによって吸収率が異なる。

目次へ ∧

5. キーホールの形成と実効ビーム吸収

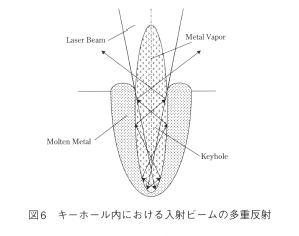
金属ターゲットに集光したレーザービームを照射すると、照射部は急速に温度が上昇し先ず溶融が始まる。その後、溶融部表面はさらに加熱されて激しい蒸発が始まる。第2章第6節に述べたように、溶融池表面は蒸発の反力によりキーホールと呼ばれる深い窪みが形成される。
キーホール内に入射したレーザービームは図6にがすように、キーホール内壁で多重反射を繰り返す。キーホール側壁へのビーム照射は斜め照射になるため、ビーム吸収は垂直照射に比べて少なくなるが、多数回の反射を繰り返す内に大部分のビームエネルギーがキーホール内で吸収される。すなわち、キーホールは一種の疑似黒体化し実効ビーム吸収は著しく増加する。
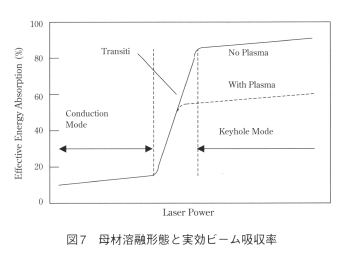
キーホールは、或るしきい値以上のレーザーパワー（正確にはパワー密度）で形成される。図7にレーザーパワーに対するターゲット材料のエネルギー吸収率の変化を模式的に示す。レーザーパワーが低い場合には、蒸発反力が弱いため表面加熱となり、垂直照射の場合に近くなりビーム吸収は低い状態である。このため母材の溶融は熱伝導型を呈する。これに対し、ビームパワーが大きくなると蒸発反力が強くなるため、キーホールが形成され実効的ビーム吸収が著しく増すようになる。ただし、図7の実線はレーザー誘起プラズマの無い場合で、レーザープラズマがある場合はプラズマ中で入射ビームの吸収が起こるため、実効エネルギー吸収は破線で示すように吸収率の増加は小さくなる。この傾向は、長波長の炭酸ガスレーザー溶接で著しいが、短波長のYAGレーザー溶接ではプラズマ吸収が殆ど生じないので実線に近い挙動を示す。

目次へ ∧

［参考文献］

1) J.F.Ready:Industrial Applications of Lasers, 2nd ed., Academic Press, San Diego (1997), p.315-334
2) P.Drude:Theory of Optics,Longmans and Green, New York (1922)
3) A.M.Prokhorov, V.I.Konov, I.Ursuand I.N.Mihailescu:Laser Heating of Metals, Adam Hilger, New York (1990),p.1-38
4) M.A.Ordal and others:Appl. Opt., 22(1983),p.1099
5) F.Dausinger and T.Rudlaff:“Novel Transformation Hardening Technique Exploiting Brewster Absorption”,LAMP’87,21一23 May, 1987, Osaka, Japan, High Temperature Society of Japan, p.323
6) F.Dausinger:ISIJI, Journal of Iron and Steel Institute International,Japan (1993)
目次へ ∧