ファラデーの誘導法則、電気に関するガウスの法則、磁気に関するガウスの法則、アンペールの回路法則における一連の積分表現はマクスウェルの方程式として知られている。電荷の存在しない自由空間が最も簡単な場合であり、四つの式は、
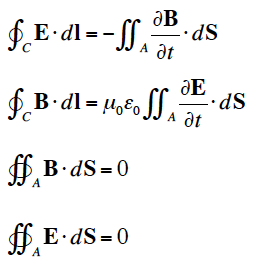
である。上式を微分形式に変換すると、第１式は
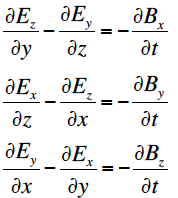
となり、第２式は
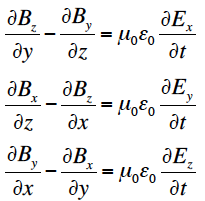
無料ユーザー登録
続きを読むにはユーザー登録が必要です。登録することで3000以上ある記事全てを無料でご覧頂けます。
SNS（Facebook, Google+）アカウントが持っているお客様は、右のサイドバーですぐにログインできます。 あるいは、既に登録されている方はユーザー名とパスワードを入力してログインしてください。
*メールアドレスの間違いが増えています。正しいメールアドレスでないとご登録が完了しないのでお気を付けください。