全半値幅中に数個の光振動しか含まないような，モノサイクルに近い極限短パルス光の発生が，すでに現実のものになっている．このような超短パルス光は，われわれに制御可能な形で与えられている高速・短時間現象のフロンティアであり，いきおい，その測定は，パルス光自体を巧みに利用して，ほかの超短パルス光またはそれ自体を測る全光タイプの計測手法によらざるをえない．

最近の波形測定技術によれば，このような間接的な手法からでも，超短パルス光の波形の詳細を知ることが可能となってきた．

本節では，このような超短パルス光の波形計測技術を概観し，併せてパルスタイミングジッタとキャリヤエンベロープ位相変化の測定にも触れる．

22・1・1 超短光パルスの時間領域と周波数領域

波動としての光を，その光電界E(t)で代表させて表す．観測される物理量としての電界は実数であるから，これを，たとえば図22・1(a)左図のように，時間tの関数としてグラフに示すことができる．「パルス」光とは，光電界の振幅が，図のように両すそに向かってゼロに近づくものをいう．電界波形の包絡線の2乗は，光パルスの強度波形I(t)に比例し，この強度波形の時間幅が，光パルスの幅である．慣用的に，強度波形I(t)の全半値幅(FWHM)を，パルス幅t_pと呼ぶ．

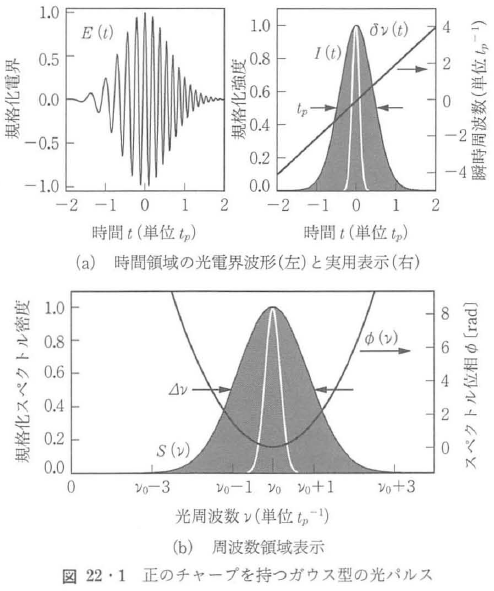
図において，光電界の振動の周期が明らかに一定でない．このように光周波数が変化する性質を，小鳥のさえずり(ピヨピヨ)にちなんで，光パルスのチャープ(chirp)とl呼んでいる．時刻とともに周波数が上昇し，パルスは正にチャープしている．チャープは，光電界の位相にかかわる現象であり，超短光パルスの波形は，この位相特性の測定を待って，初めて完全に決定される．

位相の取扱いのために，複素数の解析信号¹⁾V(t)を，E(t)=ReV(t)となるように導入する．これを極座標表示し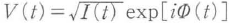と書くと，I(t)は強度波形，Φ(t)は時間領域での位相である．その時間微分ω(t)=2πν(t)=-dΦ(t)/dtは，刻々の光角周波数，すなわち瞬時角周波数を与える．

適当にとった中心周波数ν₀を起点として瞬時周波数をδ(t)=ν(t)-ν₀と書き直そう．ν₀の光振動をくくり出して，解析信号をV(t)=E(t)exp(-iω₀t)と書くとき，複索振幅E(t)を(電界の)ゆるやかに変化する包絡関数(slowly varying envelope)と呼ぶ．包絡関数の大きさは当然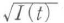である．一方，その位相はΦ(t)+ω₀tとなり時間に対して「ゆるやかに」変化する．

パルス幅が短くなっていき光振動の周期に近づくと，中心周波数を確然とは選び難くなる．このように，単一サイクル(モノサイクル)領域に近い短パルスでは，あえて包絡関数E(t)とキャリヤexp(-iω₀t)を区別する意義が消失する．さらに，Φ(t)の定数分(絶対位相)も問題となってくる．なぜなら，上述したように解析信号V(t)の実部が実体としての電界E(t)を与えるのであり，cos成分がとられるのとsin成分がとられるのとでは，E(t)が異なるからである(22・1・7でこの絶対位相の変化の計測法を述べる)．

位相Φ(t)を時間tについて整級数展開したとき，定数項は絶対位相のΦ₀，1次項は中心周波数に吸収されうる．チャープを与えるのは2次項以上である．特に，位相Φ(t)が2次関数の場合は，周波数の変化率が一定の，いわゆるリニアチャープしたパルスを与える．

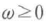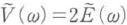すべての信号は時間領域と周波数領域の両側面を持ち，双方はフーリエ変換で結ばれている．光電界E(t)と解析信号V(t)，それぞれのフーリエ変換の関係は，に対しては，負のωに対しては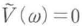となる．すなわち，解析信号の周波数領域は，光電界の周波数領域を正の周波数に制限したものに等しい．光電界について，その実数条件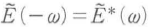から正負の周波数は独立でないので，解析信号で周波数を正に制限しても，情報が失われることはない．なお包絡関数のフーリエ変換は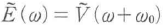であり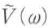，を中心周波数分だけ平行移動したものになる．

解析信号のフーリエ変換を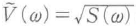exp[iφ(ω)]と書くとき，s(ω)はパワースペクトルである．また，φ(ω)はスペクトル位相(フーリエ位相)と呼ばれる．スペクトル位相φ(ω)を周波数ωについて整級数展開したとき，定数項は任意，1次項τωは，信号の時間軸上の平行移動V(t)→V(t-τ)に帰する．2次項以上が波形に実質的変化を与える．スペクトル位相φ(ω)がたかだか1次関数であるときに，一定のS(ω)のもとでの最短のパルス幅が得られ，これをフーリエ変換限界(TL : transform-limited)，またはフーリエ限界パルスと呼ぶ．

左右対称(I(t)=I(-t))の強度波形がチャープを持たないことと，左右対称の(S(ω₀+ω)=S(ω₀-ω))パワースペクトルがTLパルスであることは同値である．しかるに，いずれかが左右非対称な場合，一般に左右の成分の位相が相殺できず，チャープがなくてもTLパルスとは限らず，またTLパルスがチャープを持ちうる．図22・1(b)に，図(a)の光パルスの周波数領域を示した．図で，スペクトルは中心周波数ν₀の左右にオクターブ以上広がっているが，低周波側でゼロ周波数にまでは達していない．このすそがゼロ近傍にまでかかると，上述した絶対位相の影響が顕在化する．パワースペクトルのΔνは帯域幅とも呼ばれ，慣用的に，パワースペクトルの全半値幅(FWHM)をもって定義される．

図のスペクトル位相φ(ω)は放物線状を呈している．仮に，これがTLパルスとなった場合の強度波形を，図(a)の右図に白抜きで示した．すなわち，TLパルスの幅は元の幅t_pよりも狭くなり，スペクトル位相を補償すればパルス圧縮がおこなえる．逆に，図(a)のパルスから，強度波形を変えずにチャープを除去できたとする．元のスペクトルは，位相変調Φ(t)の分，余分に広がっている結果，チャープを除いたパルスのパワースペクトル(図(b)の白抜き)は，狭窄化する．

22・1・2 線形相関法