光パルスの圧縮は,1960年代にレーダ技術におけるパルス圧縮技術を導入してピコ秒パルス圧縮に用いたのが始まりである250)~252).ここでは,空間域レンズの相似系として時間レンズの表現を示し,位相変調と鮮速度分散補償によって時間レンズすなわちパルス圧縮が可能となることを述べる.その後,ソリトン伝搬によるファイバ圧縮,超短光パルス波形整形法とそのパルス圧縮への応用について述べる.
18・5・1 時間レンズ253)
z軸方向へのフレネル回折を考え,光電場U(x,y)のx成分のみを書き出すと,空間周波数域での伝達関数は次式で表される.
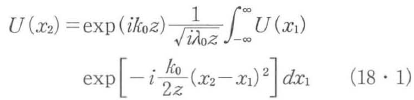
ここで,k0は光の波長をλ0としたとき2π/λ0で与えられる伝搬定数,zは伝搬方向,x1,x2は出力・入力面の座標である.このフレネル回折の伝達関数を空間周波数域で表すと次式が得られる.
![]()
ここで,kxはfxをx方向の空間周波数としたとき2πfxで与えられる伝搬定数である.exp(ik0z)の位相定数項を無視すると,この伝達関数は単純にkx2の位相シフトを受けることを意味する.すなわち,空間伝搬は空間周波数の分散を受けることと等価である.一方,中心周波数ω0の光パルスが損失のない線形媒質中を伝搬した際の伝達関数はexp[iφt(ω)]であり,位相φ(ω)は次式で与えられる.
![]()
ここで,φ0は定数項,τは群遅延,1/μは群速度分散.さらに高次の分散が加わりフェムト秒パルスにおいては無視できないが,ここでは省略する.
式(18・2)と式(18・3)を比較すると,群遅延の項を除いてはまったく同型の伝達関数になっていることがわかる.ただし,kxはω-ω0に,xはtにそれぞれ対応する.実際,入力パルス波形をフーリエ変換して式(18・3)の伝達関数を乗じ,さらにフーリエ逆変換すると,フレネル回折を空間座標で表示したと同型の次式が得られる.
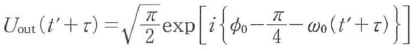
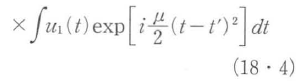
回折格子においては,群速度分散は回折格子対の間隔に比例するが,式(18・4)の1/μはフレネル回折の式(18・1)のzに対応する.つまり,z軸上での空間伝搬は回折格子による分散と表記的には等価であることになる.
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
