17・2・1 動作特性

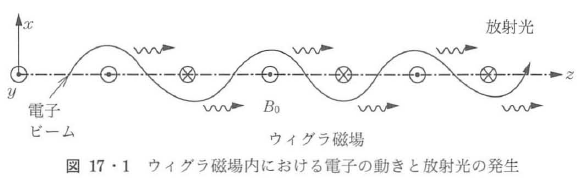
自由電子レーザーは，永久磁石や電磁石あるいは電磁波で構成される図17・1に示すような，ウィグラ(アンジユレータ(17・3・2参照))と高品質な電子ビームとの相互作用を利用して光パルスを増幅する．電磁界中の電子は加速度運動により放射光を発生することが知られている．たとえば，最大静磁界がB_wで周期長(波長)λ_w，長さL_w=N_wλ_wの平面型ウィグラからの放射光の基本周波数および放射スぺクトルは，観測者がウィグラ軸(z軸)に対して，θの傾きでy-z面(ウィグラ磁界と軸を含む面)内で観測するとして，

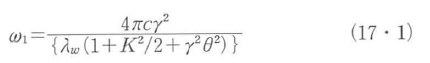
および，

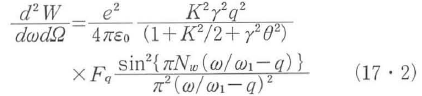
となる⁵⁾⁶⁾．ここに，q=1,3，5,・・・は，高調波の次数，K=eλ_wB_w/2πmcはウィグラの特性を示す重要な無次元パラメータ，また，γmc²(m : 電子の静止質量，c : 光速)は電子ビームのエネルギーである．

上記の放射スペクトル強度は1個の電子からの単位周波数，単位立体角当りのものである．ここに，

であり，J_mはm次のベッセル関数，ξ=K²/4(1+K²/2)である．

放射ラインスペクトル形状は基本波(q=1)に対しては図17・2のようになり，周期数N_wが大きいウィグラではω=ω₁のところに鋭いピークを持つ．このピークはウィグラによる電子の周期的運動と放射光の周期の共鳴によるものである．

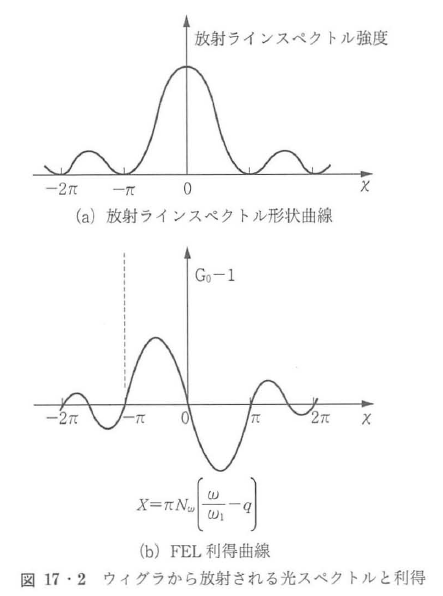
ウィグラ軸方向の電子の速度をv_zとすると，電子の振動数はv_z/λ_wとなり，そのときの電子の進行方向への放射光の周波数はドップラーシフトによりω_R=(2πv_z/λ_w)[c/(c-v_z)]となる．電子の横方向の振動速度の振幅がv₁=ck/γとなることを考えるとω_Rはω_Rは等しくなる．なお，周波数がω_em=2πc/λ_emの電磁波がウィグラとして用いられる場合，共鳴周波数は，

で，コンプトン散乱の共鳴条件に対応する．

自由電子レーザーの増幅過程は上記の自発放射と密接に関系している．

17・2・2 増幅過程