半導体レーザーは1950年代の提案，60年代の先駆的研究ののち，62年に低温パルス発振の観測，70年に室温連続発振が達成された．その後，顕著な発展を遂げ，現在では代表的な光エレクトロニクスデバイスの一つとして，光通信，光記録，光情報処理をはじめとする多くの分野で広く実用されるに至っている．本筋では，基本的な半導体レーザーの原理と構造および特性の概要について述べる^1)~10)．

13・1・1 半導体における誘導放出と光増幅利得

[1] 直接遷移形半導体のバンド構造と誘導放出条件

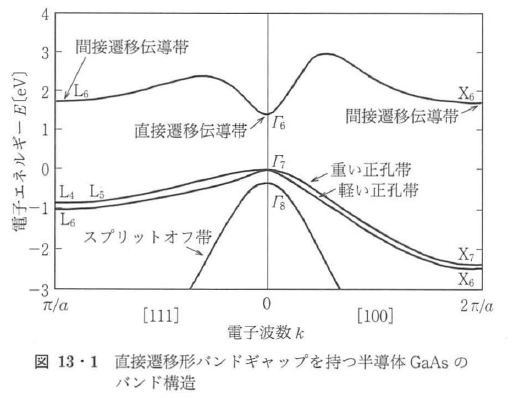
半導体レーザーは直接遷移形バンドギャップを持つ半導体中のキャリヤのバンド間光学遷移を利用して実現される．レーザー動作に必要な反転分布は光励起でも実現できるが，実用上重要な励起法は半導体ダブルヘテロ構造pn接合を形成して順電流を流し，エネルギーの高い少数キャリヤを活性層に注入する方法である．

図13・1に代表的な活性層材料であるGaAsのバンド構造を示す．レーザー作用に関与するのは，伝導帯下端近くの電子と価電子帯上端近くの重い正孔と縫い正孔である．これらのエネルギーの電子波数(運動量)k依存性E(k)は電子では下に凸，正孔では上に凸の放物(2乗)関数で近似できる．直接遷移形半導体では，伝導帯下端と電子と価電子帯上端はともにk=0の位置にあり，バンドギャップエネルギ-E_gだけ隔たっている．電子と正孔の状態密度ρ_c(E)，ρ_v(E)はそれぞれのバンド端から測ったエネルギーの平方根に比例し，図13・2のように放物線で図示される．キャリヤ注入状態における価電子帯，伝導帯のエネルギ-E₁，E₂の電子状態の占有確率f₁，f₂は，熱平衡状態での占有確率を与えるフェルミ・ディラック関数を拡張して，価電子帯と伝導帯に対して異なる擬フェルミレベルF_v，F_cを用いて，

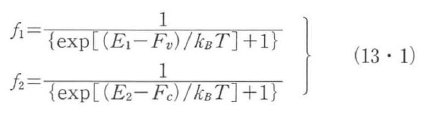
で与えられる(右図)．電子と正孔の密度は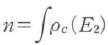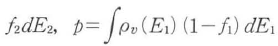で与えられn，pはイオン化不純物密度とともに電気的中性条件を満たすから，少数キャリヤ密度Nを独立変数として与えたとき，これらの式からF_v，F_cが決定される．

注入形レーザーでは，pn接合に順電圧Vを印加したとき両領域のフェルミ順位にeVのエネルギー差が与えられて少数キャリヤが注入されるので，F_c-F_vはeVに等しいE₂→E₁の遷移によりE₂-E₁=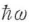のエネルギーの光子が放出されるが，この間に分布反転f₁<f₂が成立するためには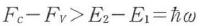が要求される．したがって，印加電圧Vは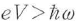を満たす必要がある．

[2] 直接遷移モデル

半導体結晶中の電子の波動関数は|ψ(r)>=|exp(ikr)u_k(r)>の形のブロッホ関数で表される．光学遷移はエネルギー保存則E₂-E₁=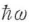を満たす必要がある．遷移確率はフェルミの黄金則で与えられ，初状態|ψ_i>と終状態|ψ_f>の双極子モーメントくψ_f|er|ψ_i>の絶対値の2乗に比例し，|ψ_f>と|ψ_f>の波数ベクトルk_iとk_fが等しい場合のみ，0でない．エネルギー保存則と波数(運動量)ベクトルが保存される遷移すなわち直接選移のみが生じる．厳密には光子運動量を含めた保存則が成り立つ遷移のみ生じるが，光子運動量は電子運動量にくらべて小さく無視できる．直接選移形半導体では上記のバンド端配置のため，キャリヤ注入により直接選移に関する反転分布が容易に実現できる．波数ベクトル範囲dk(k_i=k_f=k)の電子の遷移を考えると，単位体積当り状態数は(1/2π³)dkであり，光子放出の初状態は確率f₂で占有されており，終状態は確率1-f₁で空いている．光子放出可能な状態数は(1/2π³)f₂(1-f₁)dk，光子吸収可能な状態数は(1/2π³)f₁(1-f₁)dkである．誘導放出確率w_stmと吸収確率w_absは等しいから，正味誘導放出はw_stm(1/2π³)(1-f₂)dkをkで積分した値で与えられる．誘導放出による光波増幅の係数gは入射光子密度に対するこの放出数の比で与えられ，

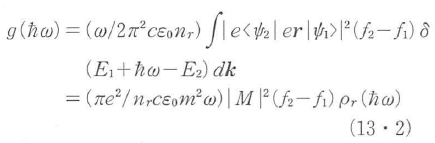
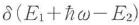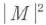
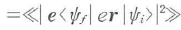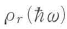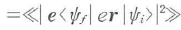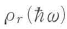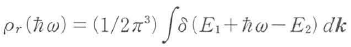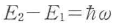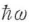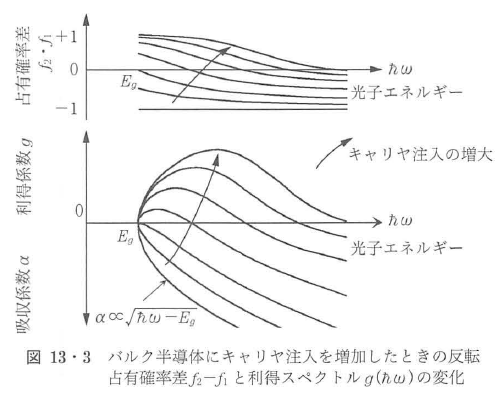
と表される．ここにωは光波角周波数，cは光速，ε₀は真空誘電率，n_rは屈折率，eとmは電子の電荷と質量，eは偏光を表す単位ベクトルである．デルタ関数はエネルギー保存則を表している．は運動量行列要素2乗平均を表す．はで定義される換算状態密度であり，E₁，E₂のk依存性が放物関数で書けるときはに比例する放物関数である．反転分布関数f₂-f₁はエネルギー保存則と運動量保存則k₂=kを同時に満たす電子と正孔のエネルギ-E₂，E₁を式(13・1)に代入することで与えられ，キャリヤ密度Nと光子エネルギーの関数である．したがって利得スペクトルg(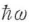)は近似的にρ_rとf₂-f₁のω依存性で決まる．図13・3にキャリヤ注入を増加していくときの利得スペクトルの変化を示す．上式と同図は，

① 少数キャリヤが注入されるとE_g近傍の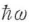の光に対して増幅利得が生じる．

② 低温ではキャリヤの利得貢献率が改善されて利得は大きくなる．

③ キャリヤ密度増大に伴って利得ピークは高エネルギー側に移動する．

などの基本的特性を示している．③はバンドフィリング効果と呼ばれる．

[3] GHLBT-SMEモデル解析と密度行列解析

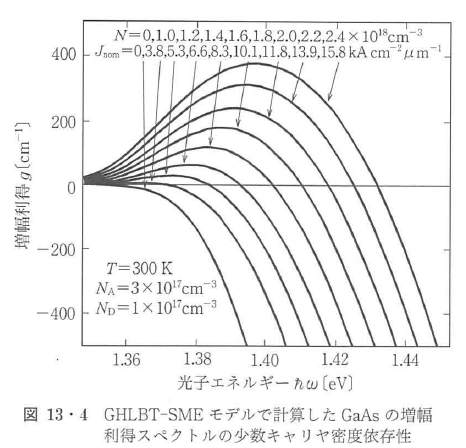
直接遷移モデルの結果は定性的には正しいが，定量的には満足な特性予測を与えない．半導体レーザーの半導体は直接遷移形ではあるが不純物がドープされているので，運動量保存則が正確に成立しない遷移も生じ，その効果が無視できないからである．このような遷移を含めた特性は始・終状態間の遷移確率をエネルギー積分する方法で解析できる．状態密度は単純な放物関数ではなく，放物関数的本休に禁制帯内に向かう指数関数的な裾(バンドテール)が加わった形となる(GHLBTモデル)．行列要素|M|²は定数ではなく，運動量差の効果およびバンドテール内電子の局在化の効果を反映して光子と電子のエネルギー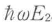，E₁に依存した値として取り扱う(SMEモデル)必要がある．さらにキャリヤ多体効果によるバンドギャップエネルギーE_gのキャリヤ密度依存性(バンドギャップ収縮)も考慮する必要がある．このようなGHLBT-SMEモデルで計算したGaAsの増幅利得スペクトルの少数キャリヤ密度依存性を図13・4に示す．

利得スペクトルは直接選移モデルの結果と同じ傾向を示すが，バンドテールの寄与のためバンドギャップエネルギー近傍では急峻な立上りではなく，なだらかなテールを伴ったスペクトルを示す．バンドフィリングはバンドギャップ収縮で一部打ち消されるが，なお前者が支配的である．

利得を得るため必要な高キャリヤ密度は電流注入で実現される．レーザー発振しきい値以下の注入レベルでは，キャリヤは主として光子自然放出に伴う再結合で消費されるが，単位時間当り自然放出数はキャリヤ密度Nの関数で与えられるので，Nは注入電流密度Jに対応づけられる．

図13・4に，対応する電流密度(活性層厚さ1 μm当りの値で表した基準電流密度J_nom)を示す．この利得スペクトルから，最大利得g_maxのキャリヤ密度依存性および注入電流依存性を知ることができる．これらはともに近似的には1次関数

て表せる．N₀(J₀)は透明化キャリヤ(電流)密度，A_g(B_g)は微分利得である．実際のレーザーでは，キャリヤは自然・誘導放出再結合以外に結晶構造の欠陥やオージェ過程による非放射再結合でも消費されるので，有効な注入電流は内部量子効率η_sp(<1)を乗じた値になる．

GHLBT-SMEモデル解析は良好な精度の結果を与えるが複雑な数値計算を必要とする．簡便で精度の良い利得解析を行う手法として密度行列解析がある．この解析では直接選移以外の効果はバンド内緩和として取り扱われ，利得スペクトルは

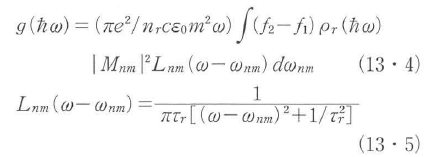
の形で書けることが示される．この結果は直接選移モデルの式(13・2)とL_nm(ω-ω_nm)のコンボリューションの形になっている．ここで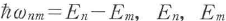は伝導帯，価電子帯電子エネルギー，τ_rは緩和時間である．L_nm(ω-ω_nm)はライン形状関数とH呼乎ばれ，τ_r→∞でL_nm(ω-ω_nm)→δ(ω-ω_nm)となる．式(13・5)のローレンツ関数の代わりにsech形の関数を用いれば精度が改善できる．多くの材料の利得特性が明らかにされている．また密度行列解析では，キャリヤエネルギー分布の擬熱平衡状態からのずれによるスペクトルホールバーニングや利得飽和などの効果も解析できる．

13・1・2 半導体量子井戸構造における誘導放出