超短パルスレーザーはピーク強度が高いため様々な非線形効果をもたらす．ここでは結晶を用いた超短パルスレーザーの2次の非線形効果による波長変換について，連続光や長いパルスにおける波長変換との違いについて述べる．フェムト秒領域における波長変換においては群遅延，位相整合波長帯域や結晶によるパルス伸長について考慮する必要が出てくる．応用例としてパラメトリック発振器について説明する．

18・7・1 超短パルス波長変換の基礎^298)299)

超短パルスレーザーの波長変換が連続光の波長変換とどのように違ってくるかを説明する．電荷のない物質中でマックスウェル方程式より導出される波動方程式は，近似的に，

であり，D=ε₀+Pである．ここで，分極Pを電場に線形な項と非線形な項に分けてP=P_L+P_NLと書き，電場の進行方向z以外の成分を0とすると

が得られる．これが非線形の基本方程式となる．

2次の非線形過程を考える．三つの電場（E_i^P,E_j^S,E_k^I）を

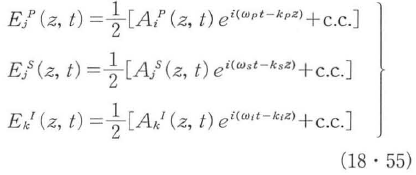
とする．非線形光学定数（d_ijk）を用いると非線形分極は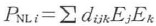で与えられる．ω_p=ω_s+ω_iの混合の場合，つまり，E_j^SとE_k^I との混合でE_i^Pが出来る場合，非線形分極のi成分は

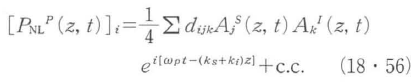
と書ける．線形の分極を考える際に超短パルス光は光周波数帯域が広いため感受率の周波数依存性を考慮する必要がある．線形感受率χ_L(ω)を中心周波数ω_pの周りでテイラー展開し第二項まで残すと線形分極は

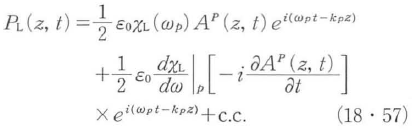
となる．この第1項のみを用いて(18・54)式を整理することにより通常の(連続光の波長変換でよく見かける)2次の非線形過程の基本方程式が得られる．

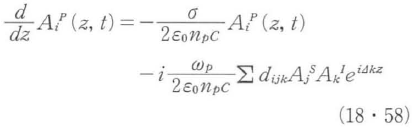
ここでΔk=k_p-(k_s+k_i)であり，これは位相整合に関係する．このときに電場振幅A(z,t)はｚとtに対してゆっくり変化すると仮定するslowly varying approximationを用いている．波長800 nmについて10 fs程度のパルス幅になってくるとこの近似を使う場合に気を使わなくてはならない領域となってくることに注意したい．また，n_p²などの関係式を用いている．

超短パルスの波長変換においては式(18・57)の第2項までを取り入れて式(18・54)を整理することにより次式を得る．

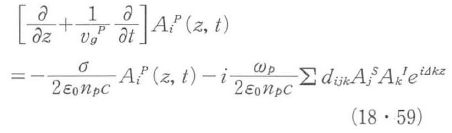
ここでv_g^Pは群速度を示す．これが超短パルスの波長変換における基本方程式となる．光電場E_j^SとE_k^Iとのクロスタームから光電場E_i^Pが生まれ，それらはi=e^iπ/2なる係数で結びついていることが分かる．ここから

という関係があることが分かる．つまり，2次の非線形光学過程による波長変換では三者の光波位相に一つの関係式が成り立つことを示す．式(18・59)は他の光についても同様に，

となる．これは三つの電場がそれぞれお互いの電場を作り出していくさまを示している．この3本の方程式を解くことによりslowly varying approximationの適用できる範囲で超短パルスの2次の非線形光学過程による波長変換は計算することが出来る．

ここで和周波光発生の様子を考えることにしよう．E_j^SとE_k^Iとから生じる和周波光E_i^Pについて考える．簡単のために光の吸収が無くパルス幅が長いときには解析的に解くことが出来る．式(18・58)式で右辺第1項を0として距離Lまでの間積分することにより和周波高強度は

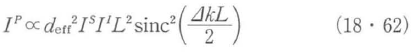
となる．つまり，E_j^SとE_k^Iとから生じる和周波光E_i^Pの強度は入射光強度の積に比例して非線形結晶の長さの2乗に比例することが分かる．また，和周波光の強度はz=π/Δk間で増加するが，その後は減少する．Δk=0となる条件を位相整合条件と言う．また，特にE_j^S=E_k^Iの時にω_p=ω_s×2となり，波長変換された光周波数は元の2倍となり，これを第二高調波発生という．

超短パルス光の波長変換については(18・59)式を用いて数値的に計算することになる．

パラメトリック増幅や発振器などを考える場合，例えばE_i^PからE_j^SとE_k^Iが発生するプロセスについても連続光の場合で光の吸収が無くポンプ光の減少が無視できる場合は式(18・61)第2,3式の左辺第2項と右辺第1項を0として第1式の左辺第2項と右辺を0とすると解析的に解くことができるが，超短パルスの場合はやはり数値計算で解くことになる．

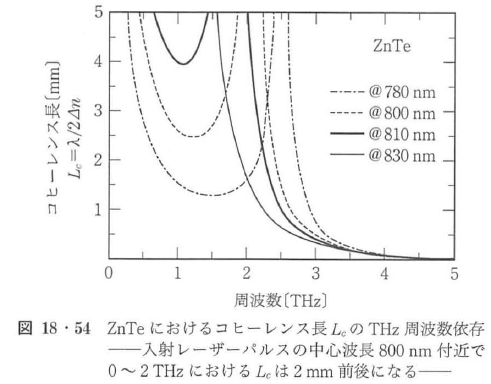
18・7・2 位相整合