重ね合わせの原理

次式で表すように、波動関数ψ₁とψ₂が微分波動方程式の解であるとする。

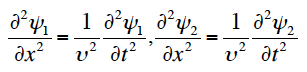
この時、

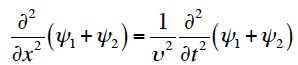
が成立するため、ψ₁+ψ₂も微分波動方程式の解となる。これを重ね合わせの原理と言う。重なり領域での波動は、各波動の代数和で与えられ(図)、共存域から外れれば重なっていたことの影響はなく、各々の波動は独立に伝搬していく。

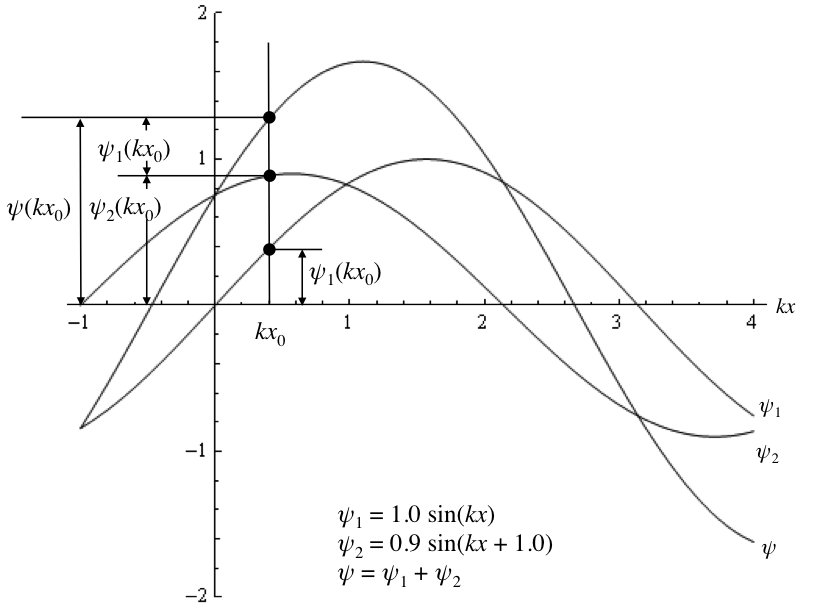
図　波長が等しく振幅が異なる二つの調和関数ψ1・ψ2とその和ψ（重ね合わせの原理）

重ね合わせの原理は広範な現象の基盤をなすものであり、定性的にでも早期に理解することが重要である。反射や屈折といった基本的現象も、膨大な数の原子による散乱波の重ね合わせとして本質的理解が可能である。

同一周波数で振幅がほぼ等しい２つの要素(正弦)波の重ね合わせを考えると、得られる合成波も、同一周波数の正弦波となる。合成波の振幅は、要素波が同位相(位相差 = 0)のときはほぼ2倍となり、要素波が逆相(位相差 = π)のときはほぼ0となる。