音波等の日常的な波動に注目すると、粒子流と比較した波動の特徴は、媒質を構成する物質が進むのではなく波動という状態(例えば、構成物質の平衡位置からの変位)が進むということである。
速度υでx軸の正方向に伝搬する波動ψ(x, t)を考える。当面、伝搬に伴う波形変化はないものとする。時刻t=0の波形をf(x)であらわすと、
t=tには波形は+x方向にυtだけ進むので、f(x)においてx→x–υtと置き換えて、
となる。上式は、１次元波動関数の最も一般的な形である。x→x+υtとすれば、-x方向に伝搬する波動を表す。
次に、ψが満たすべき微分波動方程式を求める。波動を特徴づける定数が二つ(振幅と周波数または波長)であることは、求めるべき波動方程式が２次微分を含むことを暗示している。上式から、
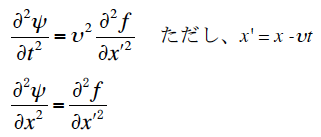
と書ける。この2式から、求める1次元の波動方程式として
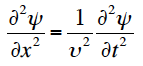
を得ることができる。