平面波の定常表現に時間依存項を導入すると、下式のようになる。
![]()
ある時刻に位相が等しい全ての点を結んで構成される面は波面とよばれる。波面上で波動関数が一定値となるのは、波面上で振幅Aが一定の場合のみである。一般にAはrの関数である。波面上でAが一定値でない波動は、不均一であるとされる。
上式で示される波動において、波面の伝搬速度である位相速度を求める。ベクトルrのk方向成分はrkである。時間dtの間に、波面がk方向にdrk移動したとすると、次式が成り立つ。
![]()
指数関数形式で書くと
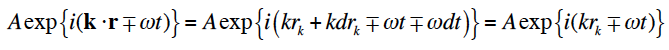
となり、kdrk=±ωdtでなかればならないことがわかる。したがって伝搬速度は下式で表現できる。
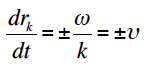
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
