平面波は3次元波動の最も単純な例である。平面波の等位相面(ある時刻に一定の位相をもつ面)は、伝搬方向に垂直な平面となる。
3次元空間中の任意点の位置ベクトルをrとすると、
![]()
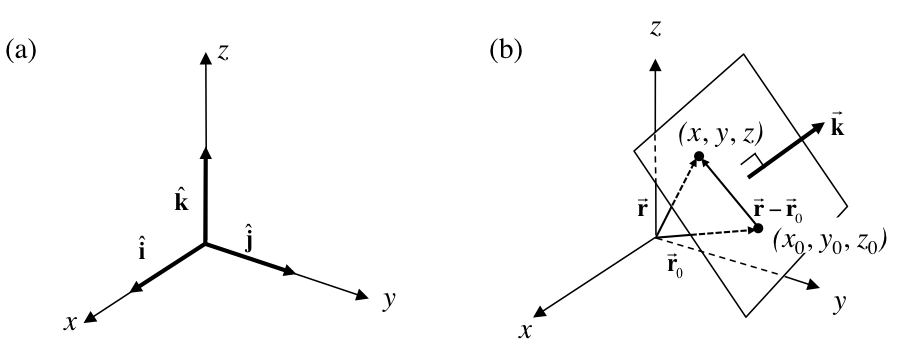
ここで、iˆ, jˆ, kˆはそれぞれ、直交座標x, y, z方向の基本ベクトルである(図(a))。
位置ベクトルr0で示される点を含みかつ、所定のベクトルkに垂直な平面を考た時、任意点の位置ベクトルをrとすると次式が成立する。
![]() …式1
…式1
図(b)からわかるように、r–r0は点r0から点rへ至るベクトルである。よって、上式はベクトルr–r0がkと直交することを示している。
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
