正弦関数・余弦関数を用いて調和波動を記述したが、本ページでは、複素指数関数で調和波動を記述することを考える。複素数 z = x + iyは、実部・虚部を座標とする複素平面上で表現できる(図2.15 (a))。極座標(r,θ)を使用することもある(図2.15 (b))。zとその複素共役数 z* は実軸に対称となる(図2.15 (c))。偏角θが時間とともに一定速度で変化するときは、回転する矢印で表現できる(図2.15 (d))。
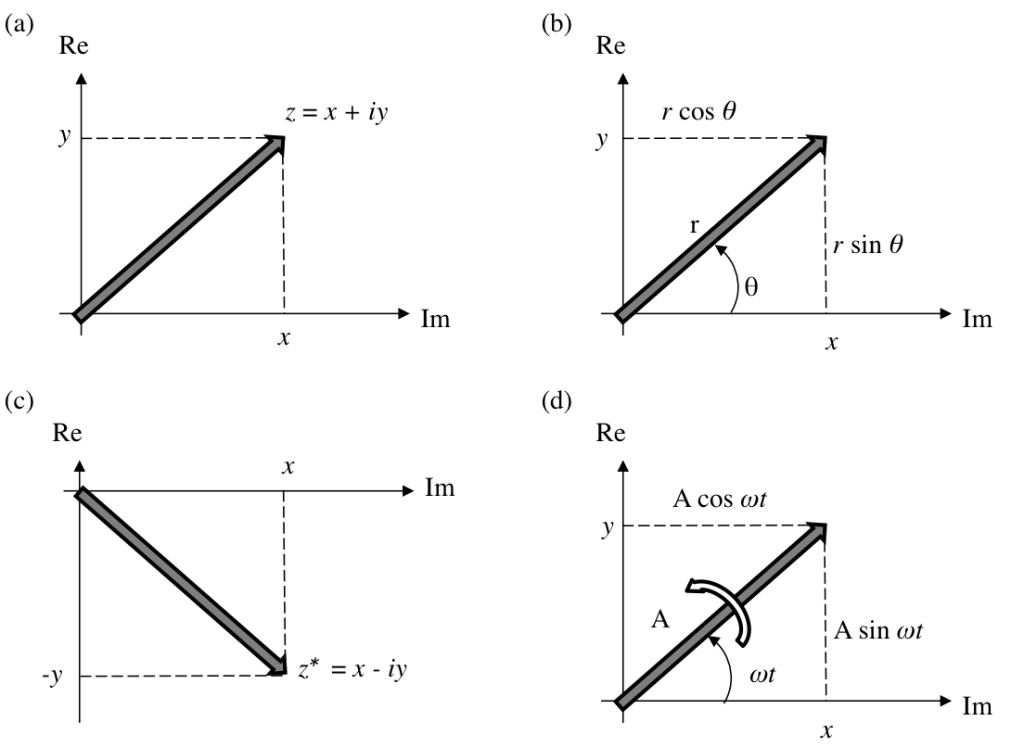
図 複素平面上での複素数 z = x+iy の表現。
(a) xとyを使用 (b)rとθを使用 (c) 複素共役数 z* (d) 偏角が一定角速度ωで変化する場合
オイラーの公式eiθ=cosθ+sinθを利用する。複素指数関数の実部で調和波動関数を表すことにすると、波動関数y(x, t)は、
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
