単位断面積当たりの伝搬パワーからわかるように、ポインティングベクトルの強度は光周波数(≈1015 Hz)の 2倍の高速で増減を繰り返す。これを実時間で計測することは不可能であり、平均化などが必要である。
ある関数f(t)の時間間隔Tでの平均値<f(t)>Tは、
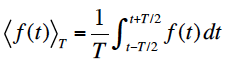
で与えられる。調和関数の平均値を求めるために、以下の計算を行う。
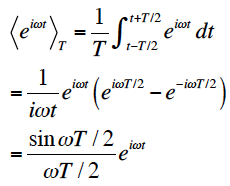
となる。sin u/uは、sinc uとよばれる(図)。上式の実部と虚部は、u=ωT/2=πとして、
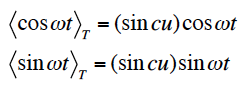
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
