電界・磁界のエネルギー密度(単位体積当たりのエネルギー)を検討する。物理的実体としてとらえた両場の基本属性を考えることになる。電界Eのエネルギー密度 uEは、コンデンサーのエネルギーを計算することで、
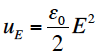
と示すことができる。同様に電流が流れているコイルを考察することで、磁界Bのエネルギー密度 uBは、
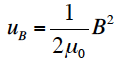
となる。前述したE=cBとc=1/(ε0μ0)1/2を用いると、上記2式から、
を得る。電磁波のエネルギー密度uは、電界と磁界が等量ずつもっており、以下の式が成立する。
無料ユーザー登録
続きを読むにはユーザー登録が必要です。登録することで3000以上ある記事全てを無料でご覧頂けます。
SNS（Facebook, Google+）アカウントが持っているお客様は、右のサイドバーですぐにログインできます。 あるいは、既に登録されている方はユーザー名とパスワードを入力してログインしてください。
*メールアドレスの間違いが増えています。正しいメールアドレスでないとご登録が完了しないのでお気を付けください。