光パラメトリック増幅器

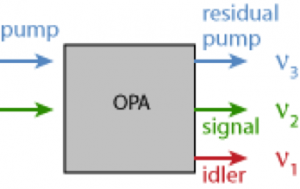
反転対称ではない結晶材料は、いわゆる2次の非線形性を示す。周波数二倍化や和・差周波発生とは別に、これは、パラメトリック増幅が可能である。信号ビームは、波長のより短い励起ビームと共に結晶内を伝搬する。励起光の光子は、(エネルギーの低い) 信号光子とそして、同じ数のいわゆるアイドラー光子に変換されます。アイドラー光の光子のエネルギーは、励起光と信号波との差である。励起エネルギーがすべて信号とアイドラービームに変換されるので、結晶材料は、この過程において加熱されない。

図 1: 光パラメトリック増幅器の模式図

通常の非縮退の場合、信号光とアイドラー光は、物理的に分かれたビームを構成する。しかし、信号光とアイドラー光が同一の縮退したパラメトリック増幅器が存在する。すなわち、同じ周波数と偏光を持つ。信号の周波数は、励起光の周波数のちょうど半分となるはずで、信号とアイドラー光の位相関係によって、エネルギーの流れる方向、つまり、信号が増幅あるいは減衰するかどうかが決まる。この位相感応増幅は、非縮退増幅器内では起こらない。任意の位相を持つ信号は増幅され、発生したアイドラーの位相は、自動的にその場に応じて調整される。 (さらなる詳細は、パラメトリック増幅に関する記事を参照。)