超高速時空間光情報処理とは，光の高速伝搬性を損なうことなく超高速光信号の処理を空間光並列処理により実現するために考案された超高速光情報処理技術である．これまでに，さまざまな原理やアイデアに基づく方式やシステムが提案され，それぞれの特徴を生かして利用されてきている．

本節では，その原理と今後の通信と処理の融合した応用に対して優れた能力を有すると思われる研究例を取り上げて紹介する．

32・3・1 スペク卜ル分解に基づく時空間変換

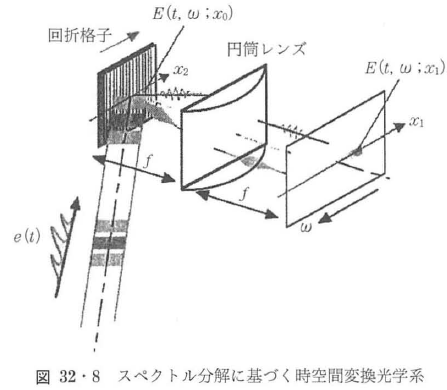
時間幅がサブピコ秒程度の極短光パルスでは，そのスペクトル幅が数十nm程度と非常に広くなる．このため，格子間隔が数μm程度の回折格子と焦点距離が数百mmのレンズを用いて極短光パルスを分光(スペクトル分解)すると，その空間的な広がりは数cmにもなる．スペクトル分解に基づく時空間変換は，この極短光パルスの持つスペクトル幅の広さに着目することにより，超高速光信号の時間に関する情報をスペクトル分布として空間的に展開し，空間光並列処理に供するインタフェース技術である^15)~17)．この技術は1980年代に提案され，超高速光信号のスペクトル分布のみの処理という自由度の低さはあるものの，その簡易性からフェムト秒レーザーの開発とともに物理・化学計測や光通信をはじめ，さまざまな分野で利用されている¹⁸⁾．その原理について簡単に説明する(図32・8)．

ω_cの中心周波数を持つ超短光パルスの光波eは，一般に次式で表される．

一方，図32・8における回折格子直後のスペクトル分解された各光波は，次式で表される．

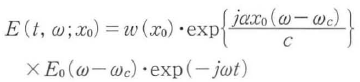
ここで，wは回折格子の窓関数，αは単位周波数変化に対する回折角度の変化量を表す．レンズを用いてフーリエ変換したのちに得られる光波分布(スペクトル分布)は，次式で表される．

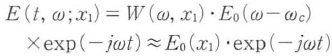
ここでWおよびE₀はそれぞれ回折格子の窓関数wと複素振幅e₀のフーリエ変換である．窓関数wの幅が十分に大きいとき，近似的にスペクトル分布は空間分布に一致する．空間展開された極短光パルスのスペクトル分布を空間的に変調し，再度対称な光学系を通して逆時空間変換を施すことにより時間波形の制御が可能となる．

32・3・2 時間およびスペクトル分解に基づく時空間変換