11・3 フォトンエコー

光の吸収・発光特性の物質による差を特徴づけるパラメータとして，発光寿命，吸収回復時間，スペクトル幅などが重要である．前者二つの定数は，エネルギー準位の分布数の変化に関係しており，エネルギー緩和と呼ばれる．一方，スペクトル幅は遷移双極子の緩和より生じ， その緩和は位相緩和と呼ばれる．位相緩和時間以内で起こる非線形光学効果はコヒーレント過渡効果と呼ばれ⁴⁶⁾⁴⁷⁾，その代表例がフォトンエコーである．不均一幅の広い吸収スペクトルを示す物質においても， このフォトンエコーにより，位相緩和時間を求めることができる．これまで種々のタイプのフォトンエコー(誘導エコー，2パルスエコー，蓄積エコー，ヘテロダインエコーなど)が開発されており，その原理，定式化については文献⁴⁶⁾⁴⁷⁾に詳しく記述されている．

ここではフォトンエコーの信号を解析するうえで通常使われている3種類のモデル，すなわち，T₁，T₂モデル，確率論的モデル，動力学的モテルの3種類の解析方法に主眼を置いてフォトンエコーを説明する．

11・3・1 T₁T₂モデル

物質のエネルギー準位を二つの準位|1>，|2>とすると，この2準位系と光との相互作用はリウヴィルの式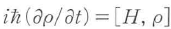で記述できる．密度行列ρはρ₁₂，ρ₂₁，ρ₁₁，ρ₂₂の四つの成分からなり，リウヴィルの式を書き下すと次のようになる．

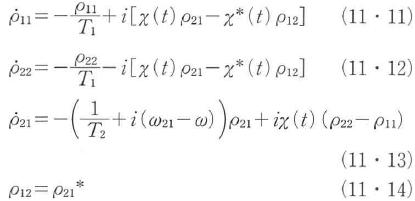
ここで，準位の寿命はT₁とし，分極の緩和時間をT₂としている．χ(t)はラビ周波数と呼ばれており，光と物質との相互作用の大きさを表している．

T₁T₂モデルではT₂は確定した定数と見るが，確率論的モデルでは熱浴のゆらぎの大きさ(Δ)とその相関時間(r_c)で表すことができる．フォトンエコーは3次の非線形光学効果であり，式(11・11)から式(11・14)を使って摂動展開により3次の分極ρ₂₁⁽³⁾(t)を求め，不均一幅について積分すると，巨視的分極が求められる．この巨視的分極を使って各種フォトンエコーの信号を計算することができる．

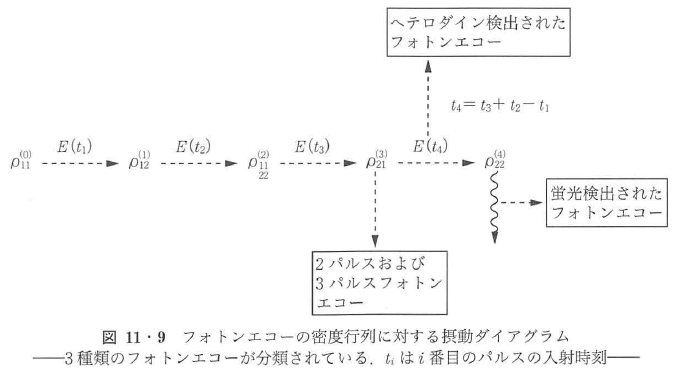
図11・9はフォトンエコーの密度行列に対する摂動ダイアグラムであり，種々のフォトンエコーが摂動の項で分類されている．ρ₁₁⁽⁰⁾(下の準位の分布)を初期条件として，1番目の光パルスにより分極ρ₁₂⁽¹⁾が作られる．2番目のパルスにより，この分極は分布ρ₁₁⁽²⁾，ρ₂₂⁽²⁾に変換される．フォトンエコーは通常は位相緩和時間の測定を目的とするものであるが，2番目のパルスにより分極が分布に変換されることから，2番目と3番目のパルス間隔T_w(待ち時間と呼ぶ)をパラメータとして信号強度を測定すれば分布の寿命T₁が測定できる．3番目のパルスにより分極が再び誘起されるが，1番目のパルスで作られた分極ρ₁₂⁽¹⁾とエルミート共役なρ₂₁⁽³⁾が誘起されれば(時間反転に対応する)遷移周波数の不均一な分布が相殺されることになる．一方，2番と3番のパルスが同時に入射(T_w=O)すれば2次の分布を作らずに直接，分極を時間反転することができる．このエコーは2パルスエコーと呼ばれており，スペクトル拡散の影響の少ない位相緩和の測定に使用される．三つのパルスを使ったエコーは3パルスエコーあるいは誘導フォトンエコーと呼ばれている．2番目のパルスで生成あるいは減少するすべての準位の分布の変化がエコーに関係することより，寿命の長い第三の準位(たとえば分子の三重項準位や準安定準位などのボトルネック準位)があると，待ち時間を2準位系の励起状態の寿命より長く設定してもエコーが再生できることになる．