分子や固体と輻射場との相互作用を議論する場合には,孤立した原子の系,たとえば原子気体を対象とする場合よりも複雑である.n個の原子核で構成されている1個の分子を考える.実際の分子では,原子核は振動している.分子は振動によって,時々刻々その形を変え,時間平均したつり合いの状態から変位した状態になっている.したがって,外部電場によって生じる双極子モーメントは,外場だけでなく,瞬間的な原子核の位置の関数となる.このことは,電子が原子核にくらべて非常に軽いので,核の運動に追随していくことができることによる.この結果,分子の電子波動関数は近似的に原子核座標をパラメータとする電子波動関数部分を核振動を表す関数部分の積で書ける.これを,この研究をおこなった研究者達の名前をとってボルン・オッペンハイマー近似と呼ぶ.
このために,分子振動に伴って,電子分布が変わり,その結果として,その変位した分子の形における電子分極率が異なってくる.この依存性を,原子核が小振幅で振動するとして,種々の分極率を原子核の変位でベキ展開する.まず一つの孤立した分子を考える.Pα(α=x,y,z)をその分子の電気双極子モーメントとしよう.これは上述したように,個々の原子核の位置(u(i))に依存する.ここでu(i)は原子核iの平衡位置からのずれを表す.pαは電場E(Eβ)の関数(β=x,y,z)でもあるので,次のように書ける.
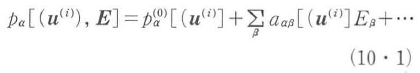
ここで,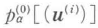 は電場がないときの電気双極子モーメントであり,0でない値をとりうる.たとえば,2原子分子の場合には,異核2原子分子は静的双極子能率を持つ.多原子分子の場合でも,対称性が低ければ,ゼロでない双極子能率を持つ.さらに,有極性分子,特に電荷移動性の置換基を持つ,いわゆる分子内電荷移動型分子ではきわめて大きい静的双極子を持つ場合がある.基底状態の静的電気双極子モーメントを,永久双極子と呼ぶ.第2項の電場の係数であるaαβ[(u(i))]は分子の1次の分極率(線形分極率)である.
は電場がないときの電気双極子モーメントであり,0でない値をとりうる.たとえば,2原子分子の場合には,異核2原子分子は静的双極子能率を持つ.多原子分子の場合でも,対称性が低ければ,ゼロでない双極子能率を持つ.さらに,有極性分子,特に電荷移動性の置換基を持つ,いわゆる分子内電荷移動型分子ではきわめて大きい静的双極子を持つ場合がある.基底状態の静的電気双極子モーメントを,永久双極子と呼ぶ.第2項の電場の係数であるaαβ[(u(i))]は分子の1次の分極率(線形分極率)である.
分子構造が反転対称性を持つ場合には,系のすべての規準振動モードは偶パリティか奇パリティのいずれかを持つ.偶パリティモードの場合,q(ν)は反転演算のもとで不変である.奇パリティモードの場合,反転演算により符号が変わりq(ν)→-q(ν)となる.図10・4に単純な線形の3原子分子の偶パリティモードを示す.
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
