6・7・1 クベルカ・ムンク理論による拡散反射

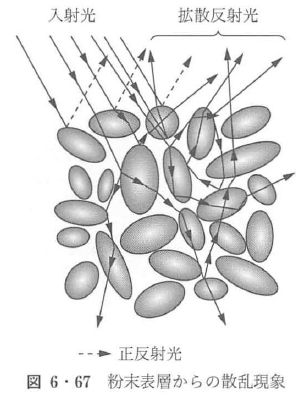
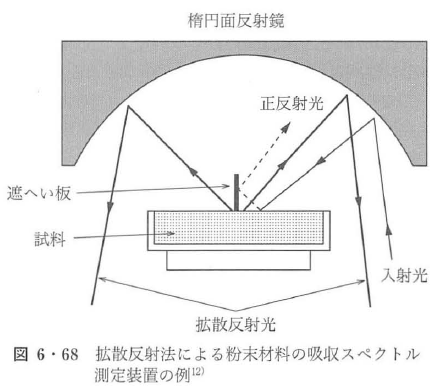
粉末や粗い表面の試料からの散乱現象は，単散乱現象とは様相が異なる．図6・67に，粉末からの散乱現象を示す．粉末からの散乱光は，粉末の表面で鏡面反射される成分と粒子に複数回散乱され粉末内部に潜り込んだのちに後方に散乱される拡散反射成分からなっている．特に，鏡面反射光は，入射光に対して反射の法則に従う方向に散乱される光であり，粉末のスペクトル特性の測定においては悪影響を与えるため測定では除去される．したがって，粉末試料のスペクトル散乱特性は，拡散反射光にクベルカ・ムンクの理論を適用することにより計測される^9)~11)．図6・68に，拡散反射法を用いた粉末試料のスペクトル測定装置の例を示す¹²⁾．図において，遮へい板は鏡面反射光を除くために設置されている．

このような拡散反射光を用いたスペクトル測定法は，クベルカとムンクによって提案された2光束理論が基礎となっている．拡散反射光は多重散乱現象であるから単散乱理論のように個々の粒子の散乱を扱うことはせずに，多重散乱の結果生じた散乱光エネルギーの伝搬に伴う現象として扱う．特に，入射光の伝搬方向に平行な前方と後方に伝搬するエネルギーのみを扱う近似理論であるとともに，i)粒子が均一に分布し，ii)粒子の外部媒質は光の吸収も散乱もなく，iii)媒質の吸収と散乱は粒子のみに依存し，iv)入射光が完全な拡散光であるという仮定のもとに成り立つ．

図6・69において，入射光の伝搬方向(z軸方向)に厚さdのスラブ状散乱媒質を考える．この媒質内の任意の位置zに想定した厚さdzの微小厚スラブ状媒質への前方光と後方光のエネルギーの流出は，次式で表現される¹³⁾．

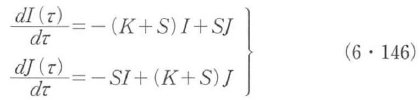
ここで，IとJはそれぞれ前方と後方に伝搬する光強度変動を表す．τは光学距離を表し，粒子の数密度と減光係数をそれぞれρとσ_tとすると，r=ρσ_tzで定義される．さらに，KとSは，それぞれ媒質の吸収係数と散乱係数である．

式(6・146)の連立微分方程式の解をe^ατと置くと，その特性方程式は，

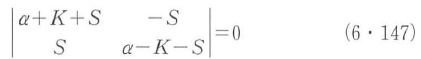
となる.このとき，係数αのとりうる値は，次式で与えられる.

よって，式(6・146)の解IとJはe^α₀τとe^-α₀τとの1次結合となり，式(6・146)ならびに厚さτ₀のスラブ状媒質のz=0とz = τ₀ = ρσ_zdにおける境界条件

を適用して未定係数を決定すると，式(6・146)の解は次式で与えられる．

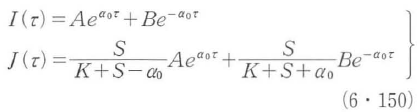
式(6・150)において，定数AとBは境界条件より，

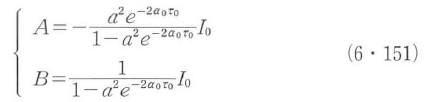
となり，a²=(K+S-α₀)/(K+5+α₀)である．