光波は波として伝搬するため,障害物によって遮られても,その背後にも回り込む.この現象を回折(diffraction)と呼ぶ.
6・4・1 ホイヘンス-フレネルの原理
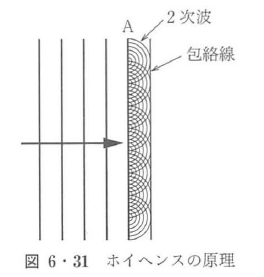
ホイヘンス(Huygens)は,2次波の概念を導入して,回折の現象を説明した.図6・31 に示すようにある時刻に波面Aが存在したときに,波面Aの各点から球面波が2次波として発生する.この2次波が互いに干渉することよって,2次波の包絡面が次の時刻の波面になる.各時刻の各波面から発生した2次波は互いに干渉するため,波の進行方向では互いに強め合うが,進行方向と逆方向に進む2次波は,互いに打ち消し合い,消える.
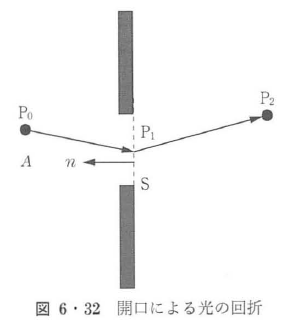
ホイヘンスの原理に基づき,図6・32に示す点P0を発した光がP2に到達する場合を記述することができる.点P0とP2の間には,開口Sが存在し,その開口上の任意の点をP1とする.点P0からは球面波が発生し,開口上の点P1に届く.開口上の各点から,2次波として球面波が発生し点P2に届くので,点P2上の光波は点P0上での振幅をAとすると,
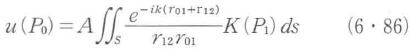
と表される.ここで,sは開口上での微小な面積要素である.K(P1)は点P1で発生する2次波の振幅が方向によって異なることと,1次波と2次波との間に位相の遅れが存在することを表す係数で,傾斜因子(inclination factor)と呼ばれる.キルヒホッフは数学的に厳密な解を求めることによって,傾斜因子K(P1)が次式で与えられることを示した.
![]()
ただし,θ1,θ2はベクトル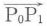 と
と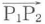 が開口の法線ベクトル
が開口の法線ベクトル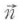 となす角である.
となす角である.
傾斜因子K(P1)は,開口の大きさに比べてr01,r12が十分大きいと仮定すると,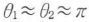 となるので,K=1/iλの定数と考えてよい.さらに,単色光について考え相対比のみを考える場合,1と考えてもよい.
となるので,K=1/iλの定数と考えてよい.さらに,単色光について考え相対比のみを考える場合,1と考えてもよい.
6・4・2 フレネル回折とフラウンホーファー回折
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
