光波は,誘電率の異なる媒質の境界面で,反射(reflection)と屈折(refraction)を生じる.この節では,二つの透明誘電体媒質の境界面に平面波が入射した場合の反射率と透過率について記述する.
6・2・1 スネルの法則
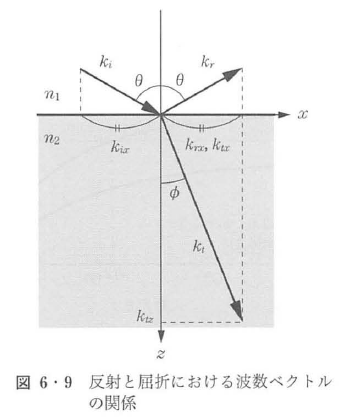
図6・8に示すように,平面波が屈折率n1の透明媒質1から屈折率n2の透明媒質2に入射したとする.境界面に垂直な方向に対して,角度θで境界面に入射し,媒質2中を角度φで伝搬するものとする.角度θとφはそれぞれ入射角および屈折角と呼ばれる.図中A点を通過する光波が境界面上のA’点に達するまでの時間は,それぞれの等位相面上の点Oを通過した光がB点を通過するまでのまでの時間に等しい.媒質1から媒質2でのそれぞれの光波の進行速度は,式(6・24)からそれぞれc0/n1,c0/n2で与えられるので,

が成り立つ.幾何学的な関係から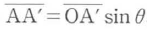 ,
, となるので,
となるので,
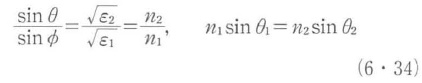
の関係が得られる.これはスネルの法則(Snell’s law)と呼ばれる.
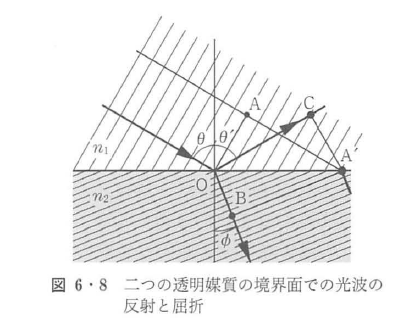
境界面での反射光の角度をθ’とすると,ABとOCがそれぞれ等位相面であるので,光波が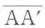 を伝搬する時間と
を伝搬する時間と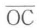 を伝搬する時間は等しい.幾何学的関係から,
を伝搬する時間は等しい.幾何学的関係から,
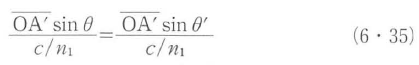
が成り立つ.任意の間隔 について,上式が成立するのでθ=θ’でなければならない.したがって,反射角は常に入射角に等しくなる.
について,上式が成立するのでθ=θ’でなければならない.したがって,反射角は常に入射角に等しくなる.
入射光,反射光,透過光の波数ベクトルをそれぞれ,ki,kr,ktと置き,x軸を境界面に平行に,z軸を境界面に垂直にとると,図6・9から波数ベクトルはそれぞれ次のように表すことができる.
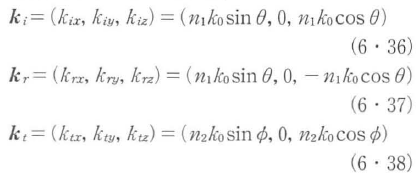
したがって,スネルの法則を用いると,
![]()
となる.以上のことから,二つの媒質の境界面で光波が反射・屈折などを生じるとき,境界面に平行な波数ベクトル成分は,反射・屈折の前後で変化しないことがわかる.
6・2・2 全反射
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
