光は波として伝搬するため，反射，屈折，回折，散乱などの現象を生じる．

本節では，マクスウェルの方程式から波動方程式を導出し，自由空間と金属中の光の伝搬について記述する．

6・1・1 波動方程式

光は電磁波の一種であるため，その性質はマクスウェルの方程式によって，記述される．

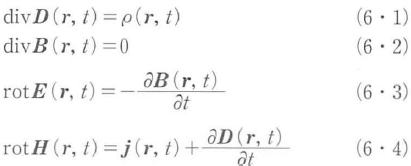
ここで，E(r,t)，D(r,t)，H(r,t)，B(r,t)はそれぞれ，電場，電束密度，磁場，磁束密度を表し，SI単位系では，[Vm^-1]，[Cm^-2]，[Am^-1]，[T=Wbm^-2]である．j(r,t)は電流密度[Am^-2]，ρ(r,t)は電荷密度[Cm^-3]である．またrは位置ベクトルである．式(6・1)は電場に関するガウスの法則，式(6・2)は磁場に関するガウスの法則，式(6・3)はファラデーの電磁誘導の法則，式(6・4)はアンペールの法則を表す．

物質の誘電率をε，透磁率をμ，電導率をσとすると，電場，電束密度，磁場，磁束密度，電流密度の間にそれぞれ次の関係が成り立つ．

誘電率εと透磁率μは，一般的にはテンソルで与えられるが，等方性の物質の場合は，スカラー量となる．真空中では誘電率ε₀は8.854×10^-12 [C²N^-2m^-1]，透磁率μ₀は4π×10^-7 [NA^-2]の値を持つ．透磁率μは，光の周波数領域では真空中の 透磁率μ₀と等しいと考えてよい．

真空中を伝搬する光は，波動方程式によって記述され，マクスウェルの方程式から導出することができる．まず，マクスウェルの方程式において，電荷密度ρと電流密度jは，真空中では存在しないため0となる．式(6・3)の両辺のrotをとり，ベクトルの公式rot rotA=grad gradA-∇²と式(6・1)および式(6・4)を用いると，電場に関する波動方程式が得られる．

同様に磁場に関する波動方程式は，次のようになる．

これらの波動方程式から，真空中を伝搬する光波の速度c₀は，

と求められる．

光波が単色光(monochromatic light)で単一角周波数ωであるすると，その光波φ(r,t)は，一般的に複素数表示を用いて，

と表されるので，波動方程式(6・8)，(6・9)に代入すると，

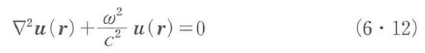
となり，時間に依存しない微分方程式となる．この方程式は，ヘルムホルツの方程式(Helmholtz equation)と呼ばれる．

また，式(6・3)と磁場Hのスカラー積と，式(6・4)にと電場Eのスカラー積との差をとり，ベクトル公式H・(rotE)-E(rotH)=div(E×H)を用いると，エネルギー保存則

が導かれる．真空中では，j=0であるので，電磁場の持つエネルギーの時間変化がE×Hの発散(divergence)と等しく，エネルギーが(E×H)の方向に伝搬することを示している．このベクトル

はポインティングベクトル(poynting vector)と呼ばれ，単位時間当り，それに直交する単位面積を横切って伝搬するエネルギーを表す．

6・1・2 平面波の伝搬