5・6・1 量子論的相関関数
量子論では物理量は演算子となるので,コヒーレンスを示す相関関数も電場演算子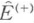 ,
,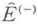 を用いて表現される.すると(5・57)に対応したn次の空間・時間相関関数は一般的に
を用いて表現される.すると(5・57)に対応したn次の空間・時間相関関数は一般的に
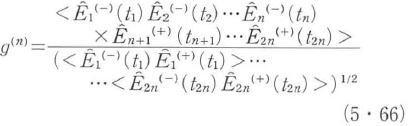
と表される.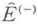 は生成演算子
は生成演算子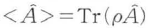 に比例する成分,
に比例する成分,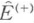 は消滅演算子
は消滅演算子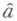 に比例する成分である.集団平均を表すは量子力学的期待値となるが,光の量子状態として純粋状態のみならず統計的な混合状態も扱うために密度演算子ρを用いて一般に
に比例する成分である.集団平均を表すは量子力学的期待値となるが,光の量子状態として純粋状態のみならず統計的な混合状態も扱うために密度演算子ρを用いて一般に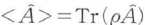 の関係から求められる.
の関係から求められる.
量子力学的なコヒーレント状態は消滅演算子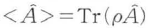 の固有状態であることから,すべてのnに対して,
の固有状態であることから,すべてのnに対して,
![]()
となることが導かれる.すなわち,コヒーレント状態は量子力学的にもすべての次数のコヒーレンスをもつことになり,このことからも理想的な古典的光波に対応する状態であることがわかる.
5・6・2 光子相関とコヒーレンス
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
