光の量子状態には古典的対応のない,あるいは古典的光波が持ちえない量子論特有の性質をもった状態がいろいろあり,新しい応用を開く光としても重要である.その代表例を述べる.
5・4・1 直交位相振幅スクイーズド状態
単一モードの光電場を
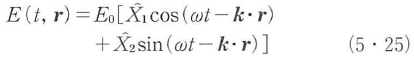
の形の量子力学的表現で表す.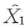 ,
,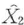 は位相が互いに90°ずれた成分の規格化実振幅に対応する演算子で,これを直交位相振幅演算子という.
は位相が互いに90°ずれた成分の規格化実振幅に対応する演算子で,これを直交位相振幅演算子という.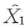 ,
,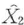 は規格化複素振幅に対応する消滅・生成演算子
は規格化複素振幅に対応する消滅・生成演算子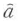 ,
,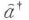 と
と
![]()
の関係にある.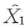 ,
,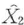 は互いに共役な物理量で,[
は互いに共役な物理量で,[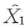 ,
,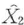 ]=i/2の交換関係を満たし,そのゆらぎΔ
]=i/2の交換関係を満たし,そのゆらぎΔ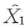 =
=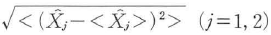 は不確定関係
は不確定関係
![]()
を満たす.コヒーレント状態では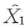 =
=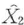 =1/2となり,最小不確定関係
=1/2となり,最小不確定関係
![]()
が満たされる.
しかし,量子状態の中には式(5・28)の関係を保ったまま,
![]()
の条件のゆらぎをもつ状態も存在し得る.一般に,最小不確定関係を満たす互いに共役な物理量のゆらぎの一方が,コヒーレント状態のゆらぎよりも小さくなる状態をスクイーズド状態(squeezed state)という.そこで,式(5・29)を満たす最小不確定状態を直交位相振幅スクイーズド状態という.
Δ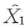 ,Δ
,Δ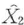 をコヒーレント状態で展開した表現で表すと,
をコヒーレント状態で展開した表現で表すと,
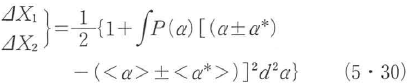
となる.P(α)はα状態の確率分布に対応する量で,古典論では正の量であるから,必ず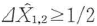 となって式(5・29)を満たす状態は生じ得ない.しかし,量子論では,前に述べたようにP(α)は負になり得るので式(5・29)を満たす状態が生じ得る.この意味で直交位相振幅スクイーズド状態は量子論特有の効果を表す非古典的状態である.
となって式(5・29)を満たす状態は生じ得ない.しかし,量子論では,前に述べたようにP(α)は負になり得るので式(5・29)を満たす状態が生じ得る.この意味で直交位相振幅スクイーズド状態は量子論特有の効果を表す非古典的状態である.
コヒーレント状態におけるゆらぎは,信号観測における通常の量子論的限界を与えるもので,これを標準量子雑音と呼ぶ.スクイーズド状態はある特定の物理量に対して,この限界を越える少ないゆらぎをもたらす.これは超高感度を要する物理測定(重力波検出など)や超低雑音光通信などへの応用上極めて重要な性質である.
直交位相振幅スクイーズド状態は,相互作用が
![]()
の形をもつ光学過程を通じて,コヒーレント状態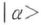 からユニタリ変換により,
からユニタリ変換により,
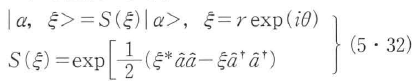
の形に生成することができる.S(ξ)はスクイージング演算子,ξはスクイージングパラメータで,r,θはスクイージングの大きさと軸の傾きを表す.これを用いてθ=0の場合の直交位相振幅成分のゆらぎを表すと,
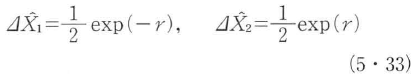
となる.式(5・31)の形の相互作用は各種の非線形光学過程を表し,これによってスクイーズド状態が実現できる.
直交位相振幅スクイーズド状態では平均光子数は
![]()
となり,同じ振幅αに対してコヒーレント状態よりも多くの光子数を必要とする.
コヒーレント状態の励起が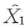 成分に対して行われた場合の,代表的なゆらぎの状態を複素平面で表したものを図5・2に示す.図(a)(Δ
成分に対して行われた場合の,代表的なゆらぎの状態を複素平面で表したものを図5・2に示す.図(a)(Δ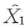 >Δ
>Δ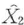 )は位相ゆらぎの小さい直交位相振幅スクイーズド状態,図(b)(Δ
)は位相ゆらぎの小さい直交位相振幅スクイーズド状態,図(b)(Δ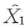 =Δ
=Δ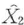 )はコヒーレント状態,図(c)(Δ
)はコヒーレント状態,図(c)(Δ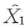 <Δ
<Δ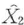 )は振幅ゆらぎの小さい直交位相振幅スクイーズド状態である.
)は振幅ゆらぎの小さい直交位相振幅スクイーズド状態である.
5・4・2 光子数位相スクイーズド状態とサブポアソン状態
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
