5・3・1 場の量子化と光子数状態
式(5・5)式で1個のモードだけを取り上げて,電磁場の時間変化を表す関数b,b*を
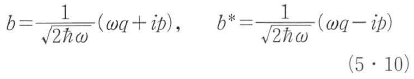
の関係によって実変数p,qに変換すると,モードを定めた空間内の電磁場のエネルギーは,
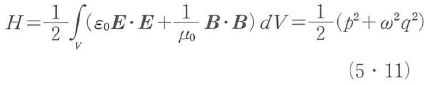
で表される.これは質量1,運動量p,座標qを持つ粒子の調和振動子のエネルギーと同じ形をしているので,これと全く同じ数学的手続きにより量子化ができる.この場合,p,qは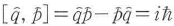 の交換関係を満たす演算子
の交換関係を満たす演算子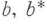 となる.また,b,b*の複素振幅a,a*も式(5・10)により[
となる.また,b,b*の複素振幅a,a*も式(5・10)により[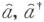 ]=1の交換関係を満たす演算子
]=1の交換関係を満たす演算子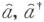 となり,式(5・11)はエネルギー演算子を表すハミルトニアン
となり,式(5・11)はエネルギー演算子を表すハミルトニアン
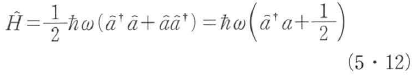
となる.ただし,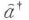 は
は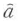 のエルミート共役を表す.
のエルミート共役を表す.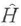 の固有値すなわち許されるエネルギー値は
の固有値すなわち許されるエネルギー値は
![]()
で与えられる.その固有状態を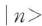 で表す.式(5・13)はエネルギーが
で表す.式(5・13)はエネルギーが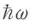 を単位とする不連続な値しか取り得ないことを表し,この状態をエネルギー
を単位とする不連続な値しか取り得ないことを表し,この状態をエネルギー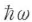 の粒子がn個ある状態と考えると都合がよい.これが光子の概念である.nは演算子
の粒子がn個ある状態と考えると都合がよい.これが光子の概念である.nは演算子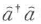 の固有値でもあるから,
の固有値でもあるから,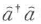 を光子数演算子という.
を光子数演算子という.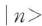 を光子数状態またはフォック(Fock)状態という.式(5・13)はn=0すなわち光子がなくても
を光子数状態またはフォック(Fock)状態という.式(5・13)はn=0すなわち光子がなくても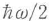 のエネルギーが存在することを表す.これをゼロ点エネルギーといい,光のゆらぎの源にもなる.
のエネルギーが存在することを表す.これをゼロ点エネルギーといい,光のゆらぎの源にもなる.
演算子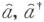 は
は
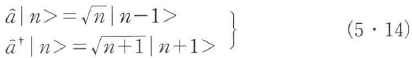
の性質をもつ.すなわち光の状態は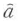 により光子数が1個少ない状態へ,
により光子数が1個少ない状態へ,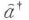 により光子数が1個多い状態へ変わる.そこで
により光子数が1個多い状態へ変わる.そこで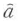 を消滅演算子,
を消滅演算子,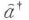 を生成演算子と呼ぶ.
を生成演算子と呼ぶ.
光子数nと光の位相φ(厳密にはn>>1でないと定義できないが)は互いに共役な物理量であり,不確定関係
![]()
が成り立つ.ΔnとΔφはそれぞれnとφのゆらぎあるいは観測に際しての不確定さを表す.光子数状態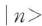 ではΔn=0であるからΔφ=∞となり,光の位相は全くわからない.
ではΔn=0であるからΔφ=∞となり,光の位相は全くわからない.
複数のモードが共存する場合は,電磁場のエネルギー値は

で与えられ,光子数状態は
![]()
で表される.
5・3・2 光のコヒーレント状態
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
