光の古典論では,光はマクスウェル方程式の解として得られる電磁場の波動により記述できる.
電場と磁束密度に対する真空中のマクスウェル方程式は
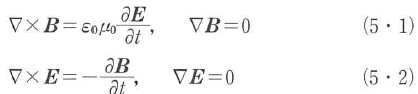
で表される.ベクトルポテンシャルAを用いて,EとBを
![]()
で表すと,式(5・1)と式(5・2)と式(5・3)よりAに対する波動方程式
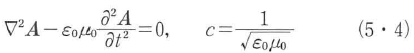
が得られる.その解から式(5・4)を用いてEとBに対する位相速度cの波動,すなわち電磁波が表される.Aの一般解を,時間関数bj(t)=ajexp(-iωjt)と規格化された空間関数uj(r)を用いて
![]()
と表すと,次のようにして式(5・4)を満たす解が得られる.uj(r)はある空間領域の,ある境界条件に対する固有値方程式の固有解として求められ,その固有値に対応して固有角周波数ωjが定まる. jで指定される各固有解をモードという.
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
