図3・4に，2枚の反射鏡を向い合せ，光をこの間の空間に閉じ込める，いわゆるファブリ・ぺロー共振器¹⁾を示す．

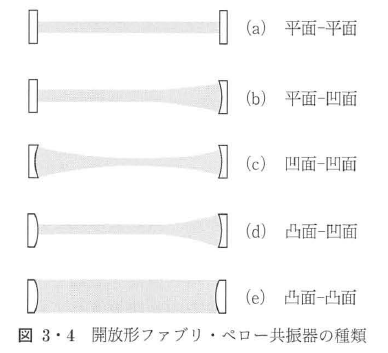
(a)の平面-平面構成は最初のルビーレーザーに用いられた²⁾が，厳密な平行度を必要とし，また回折損失も大きい．これに対し，(b)の平面-凹面，(c)の凹面-凹面構成では，回折損失も小さく気体レーザーなどによく使用される．一方，(d)，(e)の凸面鏡構成は不安定共振器(unstable resonator)と呼ばれ，回折損失は大きいが，特に(e)の構成では光の広がりが大きいため，励起された分子を有効に誘導放出に利用できるので利得が大きく，それによって光を導波することのできる固体レーザー，ガスレーザーなどにおいて大出力を得るのに使われる．

面発光半導体レーザーでは共振器長が1 μm程度と短いものの，(a)の平面-平面の開放形ファブリ・ペロー共振器が用いられることが多い．

3・3・1 共振器の安定性

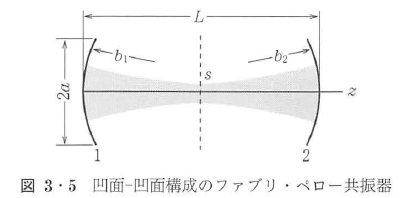
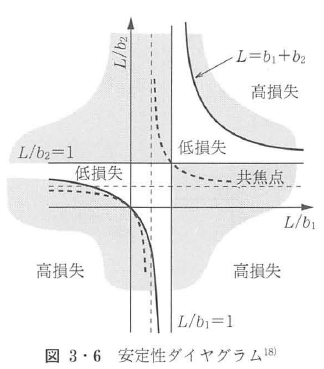
図3・4(c)の凹面-凹面構成の光の閉じ込められかたの安定性については，安定性ダイヤグラム¹⁸⁾を用いるとよい．図3・5のように左右の鏡の曲率半径をb₁，b₂，距離をLとすると，図3・6の安定性ダイヤグラムにより共振器の安定性が判定できる．このことは前に述べた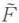マトリクスを用いて簡便に計算できる．ここでは簡単のためにb₁=b₂=2f (fは焦点距離)として，共振器の中央と反射鏡上のスポットサイズを求めてみる．共振器の中央から出発し，反射鏡2で反射されて戻った波に対する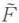マトリクスは，表3・1の自由空間と凹面鏡の要素を用いると次式となる．

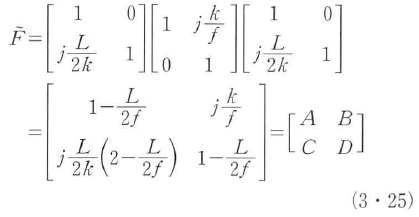
反射されて戻ってきた波の位相は平面であり，元のスポットサイズに等しいことから，波面係数Pについて，

が成り立っていなければならない．P=1/s²と置くと，この場合はA=Dであるから直ちに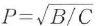となる．

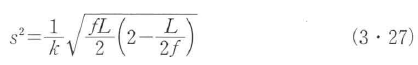
L=2f は共焦点条件と呼ばれ，sは最大値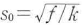をとる．したがって，

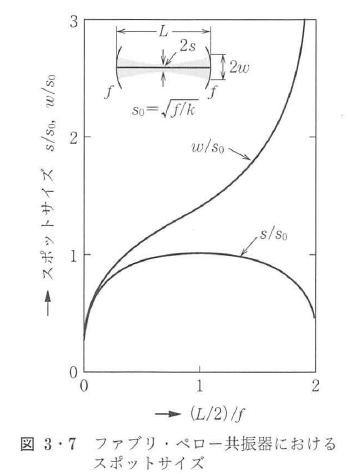
が得られる．反射鏡上のスポットサイズは，式(3・6)においてz=L/2と置いて式(3・28)を代入すると，

が得られる．図3・7にs/s₀，w/s₀をL/fに対して示す．

3・3・2 回折損失