レーザー発振器や共振形レーザー増幅器には,光を誘導放出によって増幅するレーザー媒質(あるいは活性媒質)と,光を帰還して発振の電力条件と周波数条件を満足するための共振器(電子回路における共振回路)が必要である.電子回路は1次元的な伝送線路を利用するため空間的な電磁界分布を問題にすることは少ないが,マイクロ波や光の領域では3次元的な形状を持つ共振器が用いられ,共振する周波数はもちろんのこと,空間的な電磁界に固有の分布が存在する.これらをモード(mode)という.本章ではレーザー共振器の基礎的事項を整理し,モードの概念を把握することを目的とする.
光の共振器としてはファブリ・ペロー(Fabry-Perot)干渉計と呼ばれる2枚の反射鏡が平行に置かれた共振器が知られていた1).最初のルビーレーザーでも2枚の平面鏡が用いられた2).大きさが有限の平行平面鏡対による共振器の共振モードに関する数学的な取扱いはFoxとLiにより始められた3).また,凹面鏡対による共振器が回折損失が小さいことが指摘されるとともに,いわゆるガウスモードが導出された4).その後,種々の形状のファブリ・ぺロー共振器が考えられて現在に至っている.
半導体レーザーではpn接合によるキャリヤの注入により活性化されるが,共振器として誘電体導波路を利用するのが大きな特徴である.ホモ接合の誘電体導波路としての取扱い5)を経て,より効率良く光を活性領域中に閉じ込める二重ヘテロ接合6)が導入されて室温連続動作が可能となり現在に至っている.通常は結晶の劈開7)~9)かエッチング10)11)によるファブリ・ぺロー形の共振器構成が用いられるが,単一周波数動作を目的とする分布帰還形12)あるいは分布反射形13)構成,あるいは面発光レーザー形14)も考えられている.
3・1・1 ガウス波
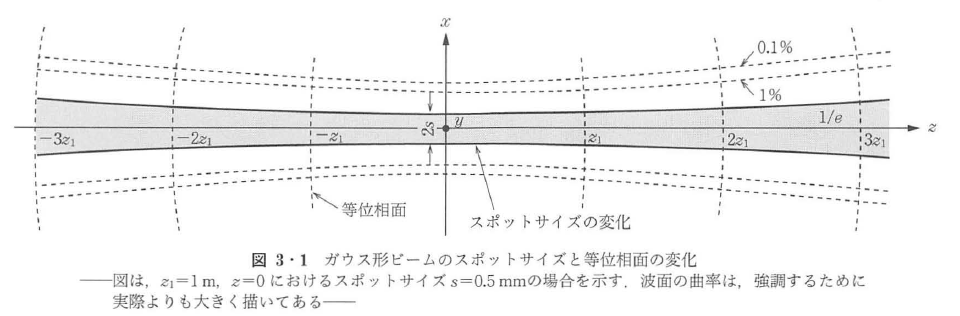
図3・1の座標系において,z=0における光の電界分布f'(x’,y’,0)は,距離zだけ一様媒質中を伝搬すると,時間因子をejωtとして,
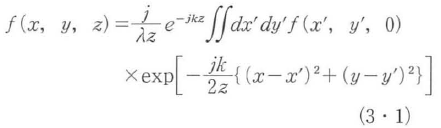
のように変換される.ただし,一様媒質中の波長をλとすると,kは伝搬定数で,
![]()
と表される.この式は簡略化されたフレネル・キルヒホッフ積分15)として知られ,光の回折を数式で表したものである.また,円筒座標で書くと次式となる.
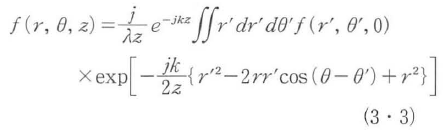
式(3・1),式(3・3)より任意の入射波に対する回折波が計算できる.横方向距離rに関してガウス分布を持ついわゆるガウス波に対する応答は積分を解析的に実行できる.スポットサイズS[注]を持つガウス波の界分布を,
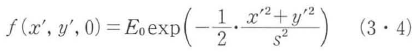
と置いて式(3・1)に代入して積分すると,
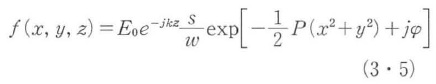
となる.ただし,

と置くと,パラメータP,φは次式となる.

式(3・5)からわかるとおり,ガウス波は回折してもやはりガウス形であり,スポットサイズと波面の曲率半径が変化する.Rが波面を表すのは,位相項exp(-jkz)を考慮し,位相が一定に保たれる条件として,
![]()
が得られ,z=-(1/2R)r2が波面を表す関数であることから理解できる.Rの符号が正のときはzの+∞方向から見て凸になっている波面を表す.
これまで随所に現れてきたパラメータz/ks2について考えてみる.これを,
![]()
と書き直し,
![]()
で定義されるNをフレネル数と呼び,光線の大きさを表すs,距離z,波長λを含む無次元量であって,光源からの相対的距離を表す量となる.

N<<1のフラウンホーファー領域では,式(3・6)のスポットサイズは,
![]()
となり,ビームの広がり角をΔθと置くと次式となる.
![]()
この式は直径Dの円形関口により回折された平面波の広がり角17)
![]()
と類似の表現となっている.図3・1にガウス波のスポットサイズ,電力が中心の1%,0.1%の位置の軌跡を示した.
3・1・2 波面係数の変換
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
