2・2・1 2準位原子とコヒーレント光との相互作用
周波数分布の広いインコヒーレン卜な光に対する誘導放出や吸収を表すには,アインシュタインのB係数が便利であるが,コヒーレントな光の場合には不便であり,また,強い光に対しては使えない.そこで次に,コヒーレントな強い光と相互作用する2準位原子の誘導放出を考える2)3). 実際の原子は,多数のエネルギー準位を持っているが,レーザー媒質ではその中の二つのエネルギー準位だけが共鳴して利用され,非共鳴の準位は不要な吸収や分散を生じている.そこで,共鳴する二つの準位だけを持つ原子を仮定し,それを2準位原子と呼んでいる.
原子の二つの準位の波動関数をψ1(r,t),ψ2(r,t)とし,固有エネルギーをそれぞれW1,W2とすれば,

と書ける.初めにいずれかの固有状態にあった原子は,入射光の摂動を受けると,
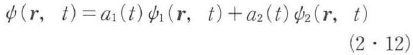
で表されるようになる.a1(t)とa2(t)は,それぞれ状態1と2の確率振動を表す.
この2準位原子に角周波数ωの直線偏光のコヒーレントな光が入射するとき,原子に働く光電界の大きさは,
![]()
と書ける.電界の方向にz軸をとれば,原子の遷移双極子モーメントのz成分は,
![]()
または,
![]()
である.ただし,e(<0)は電子の電荷を表す.
そこで,2準位原子と単色直線偏光との相互作用ハミルトニアンは,
![]()
と表される.この摂動を受けると,原子の波動関数はシュレディンガーの波動方程式
![]()
に従って変化する.ただし,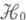 は摂動のない原子のハミルトニアンであって,
は摂動のない原子のハミルトニアンであって,

である.そこで,a1(t)とa2(t)の時間的変化は,式(2・15)と式(2・17)を式(2・16)に代入し,
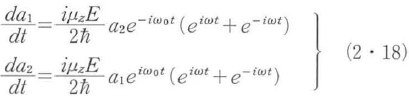
になることがわかる.exp[±i(ω+ω0)t]の項は急速に正負に振動する非共鳴項なので,無視することができる.これを回転波近似といい,この近似では,
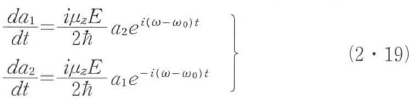
になる.ただし,式(2・15)以外の摂動はないものとする.
原子は初め上の準位にあったとして,t=0でa1=0,a2=1の初期条件のもとで式(2・19)を解くと,
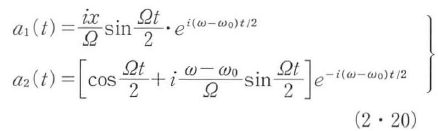
となる.ただし,

と置いた.
2・2・2 遷移確率
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
