ガス媒質を使った第三高調波の発生は古く，1969年である³⁵⁾．その後の1978年にYAGレーザーの4倍波の第七高調波³⁶⁾，1983年にKrFレーザーの第七高調波(35 nm)が得られた³⁷⁾．これらの出力は基本波の強度のq乗(第q高調波)に比例する，いわゆる摂動論の領域であった．これらはReintjesの教科書にまとめられている³⁸⁾．

高調波が新たに注目されたのは，ある次数以上で高調波強度が減少しなくなる，いわゆるプラトーの出現以降である．まず1987年にイリノイ大のグループがKrFレーザーを用いて第17³⁹⁾，フランスサクレーのグループがYAGレーザーの第33高調波を観測した⁴⁰⁾．その後，渡部らもKrFレーザーの第25高調波を観測し，波長も10 nm以下となった⁴¹⁾．短波長レーザー(KrF)を用いるとプラトーというより強度の回復が見られるのに対し，長波長レーザー(YAG)を用いるとプラトーとある次数でのカットオフが明確に観測された事実を当時は説明することはできなかった．その後，1電子近似の非摂動論的数値計算⁴²⁾や解析的手法による高調波の強度分布の説明がなされた⁴³⁾.特に後者は原子準位を無視し，基底状態と自由電子の状態のみを考え，δファンクションポテンシャルを仮定したモデルであり，これによりプラトーとカットオフをある程度説明できることから，共鳴効果は無関係であることがわかった．Kulanderらは数値計算により，カットオフエネルギーがI_p+3U_p(I_pイオン化ポテンシャル，U_p:ポンデアモーティブポテンシャル)となることを示した⁴⁴⁾．Lambropoulosのグループは，Heの数値計算から渡部らがKrFレーザーで得たデータをHeイオンの寄与によって説明した⁴⁵⁾．その間，Ti:サファイアレーザーの出現により次数は100以上まで延びた⁴⁶⁾．この結果はBeckerモデル⁴³⁾によって説明された．

得られた実験データが，数値計算や解析解からよく説明できるようになったが，物理的描像はいまだはっきりしなかった．この問題に答えたのがCorkumの2段階モデル(最近では再散乱モデルとも呼ばれる)⁴⁷⁾⁴⁸⁾．

原子の中の1電子は強電場下では瞬時に原子から解き放されるが，ある電場の位相で生成した電子は，電場によりもとの原子に引き戻される．このときに持つ運動エネルギーの最大値が3.17 U_pであり，高調波とは，戻り電子とイオン核との再結合により発生するものと考える．このモデルは2電子イオン化や高調波の偏光依存性もよく説明する．

Lewensteinらは，このモデルに従い，量子論で高次高調波の強度分布と位相を解析的に与えた⁴⁹⁾．その後，Ti:サファイアレーザーにおいて10~20 fsのパルス幅でサブTWの出力が得られるようになり，これを用いて最短波長が水の窓以下となった⁵⁰⁾⁵¹⁾．これはイオン化する寸前に瞬間的に高い電場下で高調波が発生するためである．

最近，中空ファイバ中の伝搬，自由空間における自己チャネリングにより，空間的な位相整合が得られ^52)53)54)，特定の高調波の強度が何桁も向上することがわかった．

また高次高調波による多光子イオン化が見出され，これを用いて，高次高調波のパルス幅が測定された⁵⁵⁾．高調波は強度に比例した位相シフトを受ける．その符号は光力ー効果と逆で時間領域では負のチャープをしている．この性質はまずスペクトルに現れ，基本波のチャープにより，著しい変化を示す⁵⁶⁾．また負のチャープであれば，正分散を与えれば，パルス圧縮が可能である．渡部らにより，パルス圧縮で13 fsのパルス幅が得られている⁵⁷⁾．

その後，高次高調波を用いたアト秒パルスの報告がなされた^58)~60)．これに伴いアト秒パルスの計測法の開発の努力もおこなわれている⁶¹⁾．

8・4・1 高次高調波の発生機構

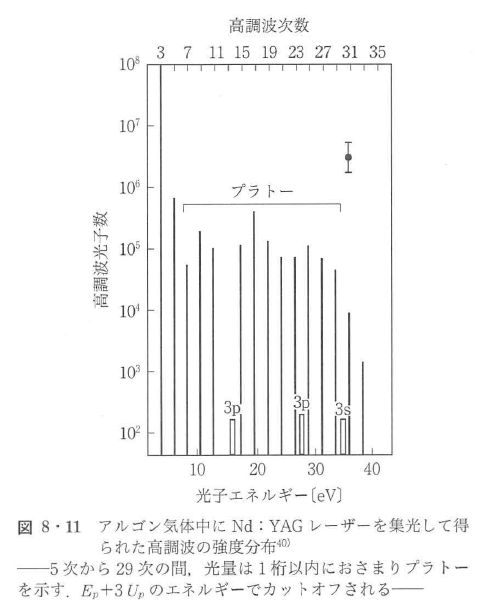
レーザー強度を増加すると，摂動論にまったく反する現象が観測された⁴⁰⁾．図8・11に示すように，3~7次まではほぼ摂動論に従い，強度は減少するが，それ以降プラトーと呼ばれるほぼ一定の強度を示す領域があり，最後に急激なカットオフが観測された．

このような新しい現象を説明するために，より基本的なところから高次高調波の発生機構を考える必要がある．

原子が位相のそろった電場にさらされるとする．原子内の1電子に注目すると，もし，この電子が自由電子なら，その運動が電場に追随する．しかし，原子内電子はクーロンカによって束縛されており，自由に動き回れない．その振動はもとの正弦波からひずみを生じ，ひずんだ双極子モーメン卜を持つ．よく知られているように，ひずんだ振動はいくつかのフーリエ成分に分解できる．このひずみのフーリエ成分が高調波に対応する．

振動電場にさらされた電子の波動関数Φ(r,t)は，

に従う．ここで，H₀は電子のハミルトニアン，Vは振動電場との相互作用を表す項で，

と表せる．ここで，mは電子質量，eは電荷，Eはレーザー電場，ωはレーザー角周波数であり，レーザーはz方向に直線偏光し，単一周波数とする．双極子モーメントの時間変化d(t)の期待値は，

と表せる．このq次高調波のフーリエ成分をD(qω)とすると観測される高調波は|D(qω)|²に比例する．この量自体は偏光面内で一定の広がりを持つ．しかし，実際には入射レーザー光と方向も位相も合った高調波のみコヒーレントに成長する．この位相整合と伝搬を考慮すると，q次高調波の光子数N_qは

と表せる．

一定の近似のもとで電子の波動関数を決めれば，高次高調波の強度は予測できる．実際数値計算例はたくさんある⁴²⁾⁴¹⁾．これらによってプラトーの出現やカットオフなどが説明できるようになった．しかし，必ずしも物理的イメージは明確でない．