10・2 自然放出ラマン散乱

自然放出ラマン散乱は，1928年にインドの研究者のラマン(C．V，Raman)によって発見された．彼は光学媒質に単色光を入射するとその波長と異なった波長が散乱されることを見出した．そのときに，いま考えると驚くことであるが，太陽光を分光して入射光とし，プリズム分光器を用いたという．この発見により，ラマンはのちにノーベル賞を受賞する．のちに詳しく研究された結果，散乱光には，一つだけでなく複数の波長の光が存在する．それらの波数の出射光のうち，長波長側の散乱光をストークス光，短波長側の散乱光を反ストークス光と呼ぶ．通常の条件下では，後者は前者よりも桁違いに弱い．この過程は通常，物質の電子および振動エネルギー準位を用いて図10・3のように表す．

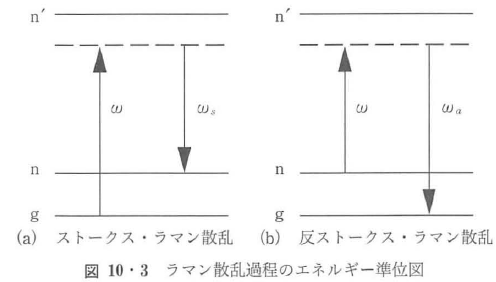
電子ラマンなどではない通常の振動ラマン過程の場合には，g，n，n’はそれぞれ基底電子状態の基底振動準位，基底電子状態の振動励起準位，電子励起状態の中の一つの振動準位を表す．周波数ωの入射光により，破線で示す仮想励起状態に遷移し，次に周波数ω_s，ω_aの散乱光を放出する．両者の強度比は，ボルツマン因子で決まる．ラマン効果は，その効果が弱く，なかなか応用範囲が広がらないと考えられていた．レーザーの出現により，このような初期の予想を逢かに超えて，現在ではきわめて広い応用範囲を持つようになった．特に科学的な分光学的応用は，発光分光，吸収分光と肩を並べるところまできている．特にラマン散乱過程は，後述するように2次光学過程であるために，通常の吸収・発光過程において禁制遷移に対応する過程が関与するため前二者と異なった状態の研究に重要な役割を果たす．たとえば分子が，反転対称性を持ち，準位が偶奇性で分類でき，図10・3においてgとn’との間の遷移双極子と，n’とnとの間の遷移双極子はともにゼロではない場合，gとn’，n’とnとはおのおの異なった偶奇性を持つ．その結果，gとnとは同じ偶奇性を持つことになるので，その間の双極子遷移は光学的に禁制であり，ラマン散乱過程は，比較的に低い確率の過程である．単位体積当りの散乱断面積は，通常1 cm^-1のオーダーである．たとえば，通常の場合，散乱媒質の中を光が10^-30 cm²/分子進んでもわずかに光子100万個に1個の割合でしか散乱されない．