光を二つに分割し,重ね合わせると明暗の縞模様が観察される.このような現象を干渉(interference)と呼び,形成された明暗の縞を干渉縞(interference fringe)と呼ぶ.干渉は,光が波動性を持つことの示す特徴的な現象である.
6・3・1 2平面波の干渉
図6・18に示すように,振幅u1で波数ベクトルk1の平面波と振幅u2で波数ベクトルk2の平面波を交差させ,干渉させる.波数ベクトルk1とk2がz軸となす角をそれぞれθ1,θ2とする.それぞれの光波は次式で与えられる.
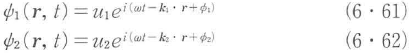
φ1とφ2はそれぞれの光波の初期位相である.これらの二つの波が重なって形成される干渉縞の強度分布I(r)は,
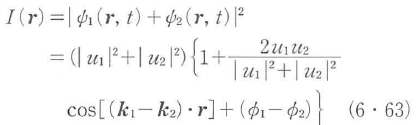
となる.干渉縞強度分布I(r)は,位置rに対して余弦波状に変化し,最大(u1+u2)2,最小(u1-u2)2をとり,平均でu12+u22となる.干渉縞のコントラスト,可視度V(visibility)は最大強度Imaxと最小強度Iminを用いて,
![]()
で定義され,u1=u2のとき可視度Vが最大1をとる.
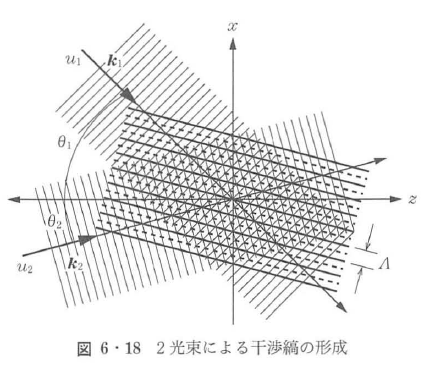
干渉縞強度分布は,(k1–k2)・rが一定となるrに対して,同じ強度をとる.したがって,干渉縞の方向は,(k1–k2)のベクトル方向に垂直方向に形成される(図6・19).また干渉縞の間隔をΛとすると,Λ=2π/|k1–k2|で与えられる.たとえば,二つの平面波がz軸に対して,同じ角度θで入射した場合,つまりθ=θ1=θ2の場合,干渉縞間隔Λは,
![]()
と求めることができる.
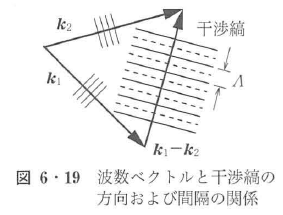
以上のことから,干渉する2光波の波数ベクトルから,形成される干渉縞の方向と間隔を容易に求めることができる.また,干渉縞の強度分布の位相は(φ1-φ2)で決まるため,干渉縞の強度分布の位相を調べることにより,二つの光波の相対的な位相分布を知ることができる.この特性は干渉計として利用される.
6・3・2 ヤングの干渉縞
無料ユーザー登録
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
