5・5・1　コヒーレンスの概念

レーザー光の示す様々な特徴はすべてそのコヒーレンス性に由来している．従ってレーザー科学においては，光の質を表すともいうべきコヒーレンスの概念が極めて重要である．

コヒーレンスは，元来，可干渉性ともいわれるように，波動の規則性の程度を表す概念として捉えると分かりやすい．しかし，光には波動性と粒子性があるし，コヒーレンス性と規則性とは必ずしも一義的には対応しないので，このように単純にはいえない．

コヒーレンスを最も一般的に表す概念は，光の場を表す物理量が，時間・空間その他の物理領域の異なる場所でどれだけ相関をもつかという性質を表すものである．従ってこれを定量的に表現する基礎になるのが各種の相関関数である．相関関数の対象となる物理量も，表現の場となる物理領域も，また相関の次数もいろいろあるのでコヒーレンスを表す尺度は一つではなく数多くある．ある特定の光を取り上げても，そのコヒーレンス性は多面的である．

5・5・2　時間コヒーレンスと空間コヒーレンス

統計的にゆらぎのある光を時間τだけずらせて重ね合わせ，その強度を観測すると干渉現象が見られる．時間関数の複素光電場E(T)を用いるとその光強度Iは

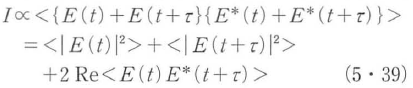
で表される． < >は集団平均または時間平均を表す．この第3項が干渉効果の現れる原因となり，干渉縞として現れる．この干渉縞の鮮明さを表す鮮明度(visibility)は干渉縞における光強度の最大値I_maxと最小値I_minを用いて，

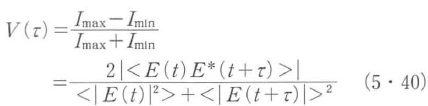
と表される．Vは0~1の値を持ち，時間的な規則性の程度すなわち時間コヒーレンスの程度を直観的によく表す量で，一般にτと共に減少する．

そこで，光の性質として時間コヒーレンスを表す基本的な量は，

で与えられる時間的な自己相関関数である．またこれを時間的な自己コヒーレンス関数ともいい，規格化した量

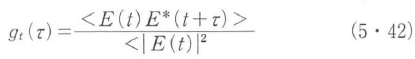
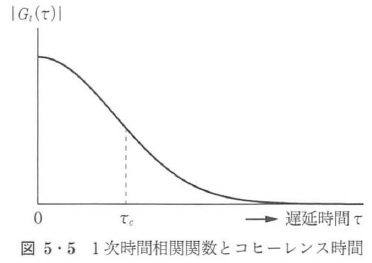
で表すことも多い．|G_t(τ)|は図5・5に示すように一般にτと共に減少し，その減少の速さが対象とする光の時間コヒーレンスを量的に表す目安となる．|G_t(τ)|が有意の値をもつτ領域の有効幅τ_cを適切に定義したもの(たとえば|G_t(τ)|が|G_t(0)|の1/2またはe^-1になるτ)をコヒーレンス時間または時間コヒーレンス長と呼ぶ．τ_c=0の極限が時間的に完全にインコヒーレントな光，τ_c=∞の極限が時間的に完全にコヒーレントな光を表す．現実の光はレーザー光でも自然光でもその中間にある．

自己相関関数G_t(τ)は，ウィーナー・キンチンの定理により，スペクトル成分の強度分布を表すパワースペクトルI(ω)とフーリエ変換の関係にあり，

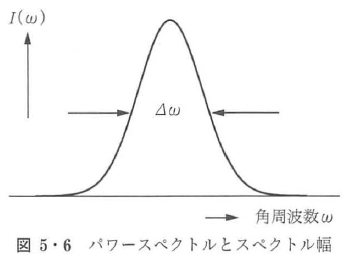
と表される．I(ω)はE(t)のフーリエ周波数成分E(ω)と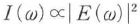の関係にある．式(5・43)より，適切に定義されたスペクトルの有効幅Δω(図5・6参照)とコヒーレンス時間τ_cとの間には，

の関係が成り立つことが導かれる．すなわち，スペクトル幅の大小が時間コヒーレンスを反映することになる．時間コヒーレンスのよい(τ_cの長い)レーザー光は単色性のよい(Δωの狭い)光となり，時間コヒーレンスの悪い(τ_cの短い)自然光は広いスペクトル幅の光となる．

次に空間の異なる場所における光電場の相関，すなわち空間コヒーレンスを取り上げる．空間は三次元であるが，光の伝搬方向の空間的諸性質は時間的性質を変換したものであり，したがって，この座標成分における空間コヒーレンスは時間コヒーレンスと本質的に同じであって，特に新しいことはない．問題にすべきは伝搬方向と直交する空間座標における空間コヒーレンスである．今後，特に断らない限り，空間コヒーレンスとはこの座標成分に関するものを意味することとし，その空間座標を代表的にxで表す．