2・4・1 基礎方程式
光共振器には無限個のモードがある(3章参照).レーザー共振器の中の光電界はレーザー媒質によって増幅され,共振器の損失とレーザー出力の取出しによって減衰する.そこで,レーザー発振するのは増幅が減衰を上回る有限個のモードである.レーザ一発振しているモードλの固有関数をUλ(r),発振周波数をωλとすれば,共振器内の光電界E(r,t)と物質の分極P(r,t)は,
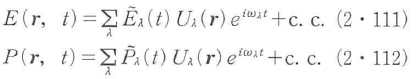
と書ける.ここで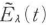 と
と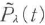 にくらべるとずっとゆっくり変わる関数である.モードλの固有周波数をΩλ,振幅減衰定数をαλとすれば,マクスウェルの式から,
にくらべるとずっとゆっくり変わる関数である.モードλの固有周波数をΩλ,振幅減衰定数をαλとすれば,マクスウェルの式から,
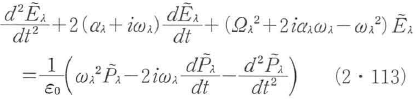
である.
いま,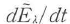 と
と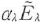 は
は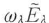 にくらべて小さい場合,高次の微小量を無視すると,式(2・113)は回転波近似で,
にくらべて小さい場合,高次の微小量を無視すると,式(2・113)は回転波近似で,
![]()
となる.
一方,2準位原子のレーザー媒質の分極はP=Nμz(ρ12十ρ12*),反転分布はI=N(ρ22-ρ11)であるが,これらの空間的分布は不均一であるから,それぞれP(r,t),I(r)と表す.式(2・37)と式(2・38)を式(2・111)および式(2・112)を用いて書き改めると,回転波近似では,
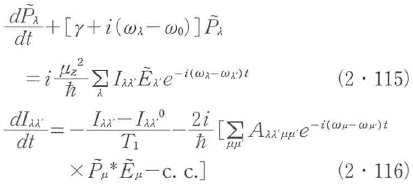
となる.ただし,Iλλ’とAλλ’μμ’はモード関数の重なり積分
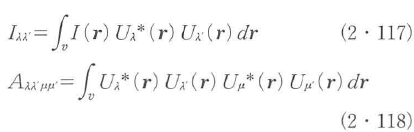
で定義されている.
2・4・2 単一モード発振
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
