2・3・1 基礎方程式

レーザーは，広義の光共振器(3章参照)の中にレーザー媒質を入れ，それを励起(ポンピングともいう)して反転分布状態にしたものである．共振器の中の光は，共振器の損失によって減衰すると同時に，反転分布媒質によって増幅される．このとき，増幅率が減衰率を上回れば，レーザー発振が起こる．レーザー発振の主な特性は，レーザー光の強度とレーザー媒質の各準位の原子数とについてのレート方程式(速度方程式ということもある)によって，次のように論じることができる．

レーザー共振器の一つの共振モードに存在する光子数をn，共振器のモード体積の中にある2準位原子の反転分布をIとすれば，それらの時間的変化は，

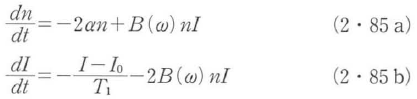
と表すことができる．ここに，2αは共振エネルギーの減衰定数，T₁は2準位原子の反転分布の緩和時間すなわち2準位の縦の緩和時間，B(ω)は単一周波数ωの光子による誘導放出係数であって，不均一広がりがなければ

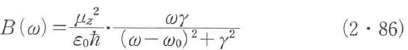
となることは式(2・72)からわかる．不均一広がりがあるときには，式(2・79)や式(2・80)から求めなければならないが，近似的には上式のyの代わりに不均一広がりを含む等価的な幅を使うことができる．

式(2・85a)では，自然放出は小さいものとして無視されている．普通の固体レーザーや気体レーザーではそれでよいが，半導体レーザーや色素レーザーではレーザーモードの光子数の自然放出による増加が比較的大きいので，式(2・85a)に自然放出を表す項を付加する必要がある．

アインシュタインのB係数(2・1・1参照)は，光子数ではなくて光のエネルギー密度について表したものであるから，式(2・29a)と式(2・86)との間には，

の関係がある．

レーザー媒質の励起や緩和の過程を取り扱うためには，2準位以外のほかの準位の原子数も変数として，上と同様の考え方で多次元のレート方程式を書くことができる．この場合，レーザー遷移に関与する2準位以外にはレーザー光や反転分布に直接の影響がないものとすれば，レーザーの動作特性については近似的に式(2・85)のレート方程式に帰着して論じることができる．

レート方程式では光の位相を取り扱わないので，レーザー発振周波数の変化や同期現象，あるいは多モード発振について論じることはできない．また，光子数や反転分布原子の共振器内の空間的分布が影響するような問題には適用することができない．このことは，レート方程式は共振器内を光が往復する時間よりも短時間の変化を論じるのには不適当であることを意味する．その代表的な例はモード同期やモード競合である(2・5節参照)．

2・3・2 定常発振