6・6・1 ミー散乱理論の展開

光の散乱現象は，散乱体のサイズや光学的特性に応じて回折，屈折，吸収，およびそれらが結合して現れる電磁光学的な現象である．ミー(Mie)は，単色平面波の均一媒質内にある1個の伝導球による回折現象を電磁気学的に取り扱い厳密解を得た¹⁾．光の散乱場は，式(6・1)～式(6・4)のマクスウェル方程式から導かれるベクトル波動方程式で表される．伝導球への入射場，内部場，および散乱場を球面波展開し，さらにヘルツベクトルを導入することによって，極座標形式のスカラー波動方程式を得る．このスカラー波動方程式を，動径，天頂角，方位角の3変数に関して変数分離し，それぞれの変数に関する微分方程式の解析解を得る．スカラー波動方程式の解として，伝導球の内部場と散乱場のそれぞれの解が伝導球の中心と無限遠においてゼロに収束するように3変数の解の1次結合をおこなう．最終的には，ヘルツベクトルから伝導球の内部場と散乱場の厳格解を得る^2)~9)．ミー理論は球体にのみ適用可能であるにもかかわらず，現代においても非常に有用な理論である．特に，近年のマイクロコンピュータのハードウェアとソフトウェアの急激な発達によって，簡単・高速に数値計算が可能となり，その有用性はむしろ増大している．

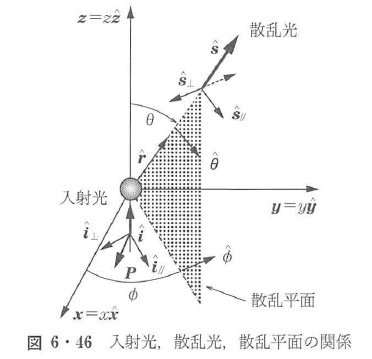
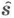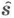図6・46において，x軸方向に偏光した波長λの平面波が，z軸に沿って球粒子に入射する．球粒子の半径はa，屈折率はn₁とする．周囲の媒質は吸収がなく，その屈折率はn₂とする．図に示すように，入射平面波の偏光方向(x軸)と進行方向(z軸)によって定義される直角座標系において，球粒子は原点にあるものとする．散乱方向を単位ベクトルで表し，と単色平面波の入射方向(z軸)で形成される平面を散乱平面という．散乱角は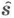，とz軸の正方向とのなす天頂角θと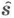のxy平面への投影とx軸の正方向とのなす方位角φからなる．このとき，球粒子の遠方放射場における散乱光振幅のφとθ方向成分は，ミー散乱理論によると次式で与えられる．

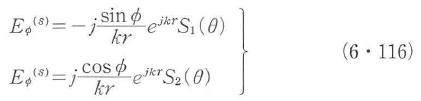
ここで，S₁とS₂は散乱振幅行列の要素を表し散乱振幅と呼ばれ，次式で定義されている²⁾．

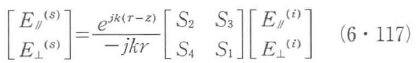
散乱体が球のときにはS₃=S₄=0であり，S₁とS₂は次式で与えられる．

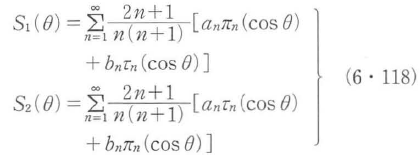
ここで，a_nとb_nは散乱係数と呼ばれ，伝導球の粒径パラメータα = 2πa/λと相対屈折率m = n₁/n₂を変数とするリカティ・ベッセル関数φ_nとχ_n，その1次結合である球ハンケル関数ξ_nおよびそれぞれの1階微分を用いて，次式で与えられる．

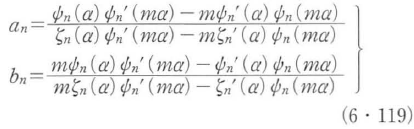
ここで，πとτは角関数と呼ばれ，ルジャンドル陪関数とその散乱角θに関する1階微分によって次式で与えられる．

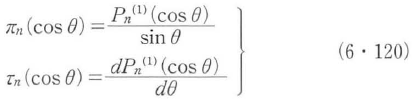
さらに，散乱光強度のφとθ方向成分は，

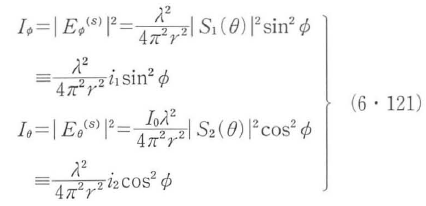
となる．ここでi₁とi₂は強度関数と呼ばれ，それぞれ散乱平面に垂直な成分と平行な成分の散乱関数を表し，強度の次元を持っている．すなわち，図6・47(a)に示すように，入射光の偏光方向が散乱平面に垂直であるとき，散乱平面がyz平面に一致するのでφ=90°となる．このような散乱光の偏光状態をs偏光と呼び，その散乱強度は，

となる．一方，図(b)に示すように入射光の偏光方向が散乱面に平行のとき，散乱面がxz平面に一致するのでφ=0となる．このような散乱光の偏光状態をp偏光と呼び，その散乱強度は次式となる．

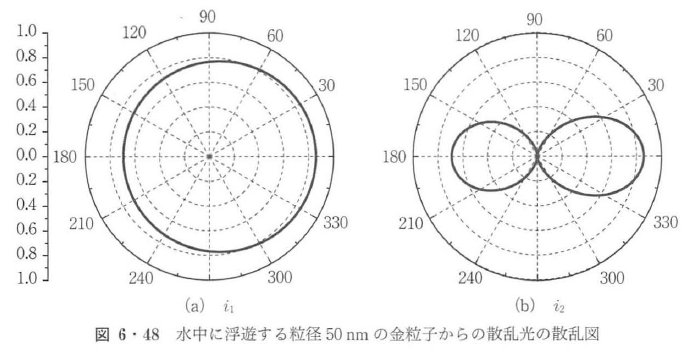
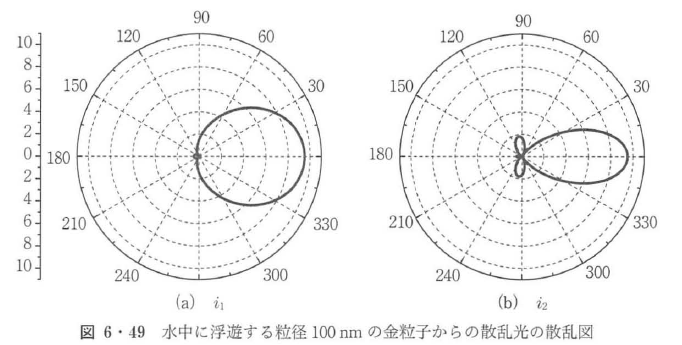
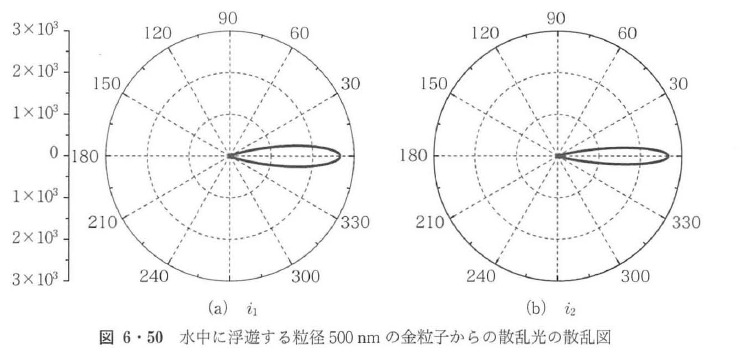
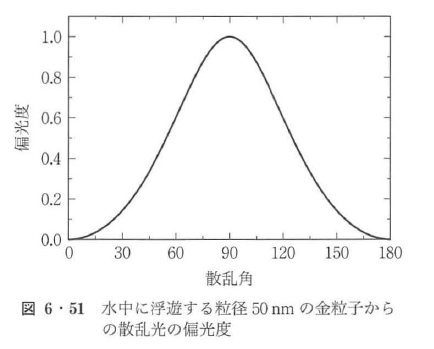
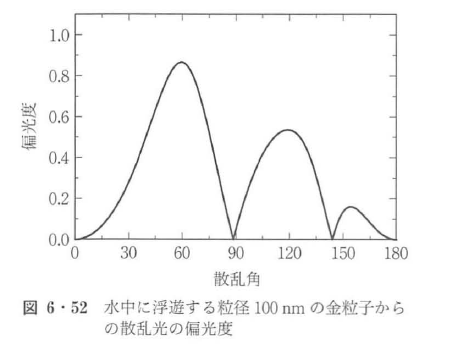
図6・48~図6・50に，波長550 nmの単色平面波によって照射された水中の金粒子からの散乱現象の散乱図を示す．ここで，水の屈折率は1.33，金粒子の複素屈折率は0.57+j2.45であり，3種類の粒子径50 nm，10 nm，500 nmについて計算をした．図より，粒径500 nmのような波長と同程度の粒径では，前方散乱が後方散乱にくらべて極端に支配的になり，散乱光エネルギーは散乱角±15°以下の領域に集中している．粒径が減少すると散乱光エネルギーの角度分布が広がるとともに後方散乱の寄与が増加する．p偏光成分は前方と後方に散乱光エネルギーが集中し，s偏光成分のエネルギー分布は等方的になる．さらに，粒径が減少し，波長の1/10以下になるとp偏光成分は前方と後方に等しく散乱光エネルギーが集中し，s偏光成分のエネルギー分布は完全に等方的になり，レイリー散乱の散乱図となる．

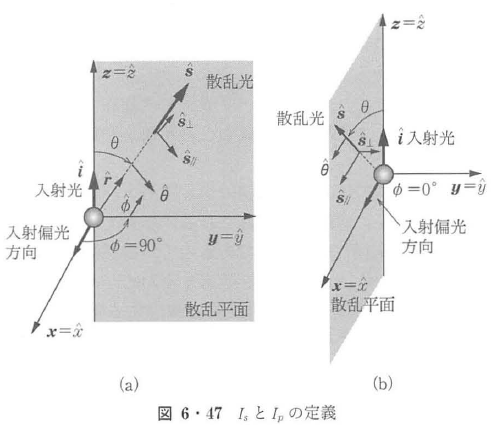
自然光の散乱強度は，自然光が無偏光状態であることから，偏光した散乱光の式をすべての偏向角に関して平均する必要がある．すなわち，式(6・121)より，

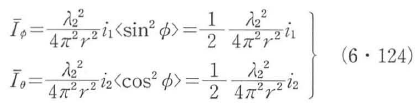
となる．散乱強度i₁とi₂は一般に0ではないので，散乱光は部分偏光状態にあり，その散乱強度と偏光度はそれぞれ次式となる．

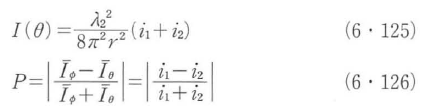
図6・51~図6・53には，図6・48~図6・50に示した波長550 nmの単色平面波によって照射された水中の金粒子からの散乱光の散乱図に対応する偏光度を示す．図より，粒径が50 nmでは近似的にレイリー散乱の偏光度になるが，粒径が増加するに従って偏光度は複雑に変化することがわかる．

6・6・2 ミー散乱理論を利用した粒子径計測