媒質のエネルギー準位間に共鳴するようなレーザー光を入射すると，共鳴吸収によりエネルギーは散逸し，透過光は減衰してしまう．しかし，ある種の媒質においては，第二の制御光を入射し，周波数をうまく選ぶことにより，第一の光の減衰が回復し，媒質は透明になることが知られている．この現象を電磁誘導透過(electromagnetically induced transparency:EIT)と呼び，典型的な多準位多光波の系における非線形光学現象として注目を浴びている．

従来の量子光学における原子と光の相互作用の研究は，2準位系原子と1光波の相互作用が主流であった．たとえば，光の吸収や分散，誘導放出，レーザー発振などの諸現象や，飽和吸収などの非線形分光，あるいはラビ振動，フォトンエコーなどのコヒーレント過渡現象などは，この範疇で論じられる．これに対し，多準位系原子と多光波のコヒーレントな相互作用は，これらとは異なる，新しい物理学と興味ある現象を提示してくれる．多準位系の場合，素過程として複数の量子力学的な経路を含み，それらが干渉を起こす，いわゆる量子干渉効果が生じ，その代表となるものがEITである．

以下にEITの原理とそれに関する種々の話題と応用例を述べる．

11・2・1 暗状態

最も一般的な系として，3準位系と2光波の共鳴相互作用を考えよう．エネルギー準位配置としては，図11・5のように3準位のうちのどの準位間に共鳴光が入るかにより，(a)Λ型，(b)V型，(c)カスケード型(はしご型)がある．このうち最もポピュラーで，かつ応用上も重要なものがΛ型である(以後Λ型に話を限定する)．また，照射される2光波を，図(a)のように，プローブ光，カップリング光と呼ぶ．

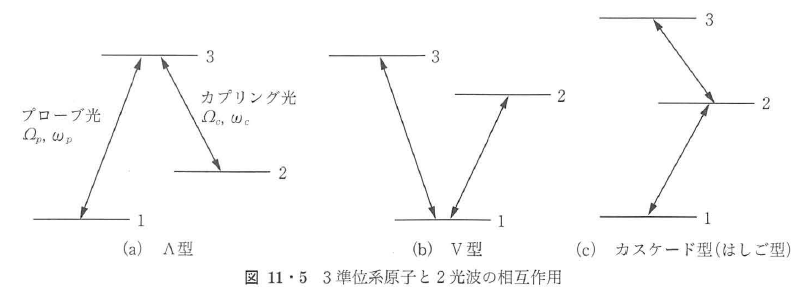
3準位系と2光波の相互作用は密度行列の運動方程式に緩和項を加えたリウヴィル(Liouville)方程式で運動が記述できる．このような3行3列の密度行列の場合，各成分として，各準位の分布数(n₁,n₂,n₃)と三つのコヒーレンス(二つの光遷移コヒーレンスρ₁₃，ρ₂₃と一つのサブレベルコヒーレンスρ₁₂)で原子の挙動が決まる．実際にリウヴイル方程式を解くと，下準位|1>と|2>の寿命，およびサブレベルコヒーレンスρ₁₂の緩和速度を無視し，2光子共鳴の条件(ω_p-ω_c=ω₂₁)のもとで，定常状態における系の波動関数は，

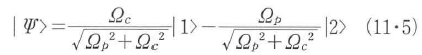
となることがわかる．ここで，Ω_p，Ω_cはプローブ光，カップリング光のラビ周波数である．

この解は，励起準位|3>からの寿命や，コヒーレンスρ₁₃やρ₂₃の位相緩和時間をたとえ考慮しても，その値にかかわらず成立することに，特に注目したい．式(11・5)の状態は，暗状態(dark state)と呼ばれ，数々の興味ある特徴を包含している．まず，定常状態が(密度行列ではなく)波動関数で表現されている，すなわち，系は混合状態ではなく純粋状態である．また，この系は，緩和が伴わないからエネルギーの散逸もない．式(11・5)において，励起準位|3>の確率振幅はゼロであるから，励起準位の分布数はゼロ，したがってこの系から蛍光は観測されない²⁶⁾(この事実が暗状態と呼ばれるゆえんである)．分布数は，下の二つの準位で比率n₁/n₂=|Ω_c|²/|Ω_p|²をもって分配される．分布数がこのように励起準位に移行できないような状態を特別にコヒーレントポピユレーショントラッピング(coherent population trapping)ともいう(このような分布数が下の2準位に固定された状態は． 1光子反跳限界温度以下に原子をレーザー冷却する技術としても利用されている²⁷⁾)．また，準位|3>の振幅がゼロだからコヒーレンスρ¹³，ρ²³もゼロであり，これは，カップリング光，プローブ光とも吸収を受けずに伝搬していくことを示唆している(EIT)(蛍光の消失と透過光の透明化は，表裏一体の現象であることに注意したい)．

以上のような暗状態の生成は3準位系に特殊なもので，2準位系においては実現しえない．よく知られる2準位系の定常状態は混合状態であり，多かれ少なかれ分布数は励起準位に移行し，自然放出などによりエネルギーが散逸する．これに対し，3準位系におけるこのような暗状態の生成は，以下に述べる種々の現象の基礎として重要な意味を持つ．

11・2・2 電磁誘導透過