分子振動座標は，規準振動モード関数と呼ばれる規格完全直交系で展開され，あらゆる振動は，それを構成するモードの線形結合で記述することができる．この完全直交系の各モードは，調和振動子で記述される．調和振動子の量子化に従って分子振動を量子化する．
分子の規準振動モードの固有エネルギーである振動準位エネルギーは量子化され，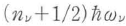
(nν：整数)で与えられる．量子準位nνにある分子に，周波数ωIで入射した光子が散乱され，分子をnν+1の振動準位に励起し，それに伴って
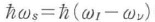のエネルギーの光子が散乱される．これがストークス散乱である．反ストークス散乱の場合には，分子はnνからnν-lに脱励起され，散乱光子のエネルギーは，
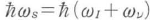となる．体積Vの中にある分子を座標系の原点にあるとする．そのハミルトニアンは，輻射場のハミルトニアン6)
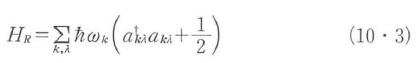
から構成される．ここで，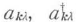
は，波数k，偏光λの光子の消滅・生成の演算子である．よって振動分子のハミルトニアン
を得る．ここで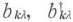
は，調和振動子の量子準位間の下降・上昇の演算子である．
ラマン非線形性は，輻射場の電場と分子振動分極との聞の相互作用により，レーザー駆動場と分子振動が結合する．電場中の分極した双極子と電場との相互作用エネルギーは，古典論的ハミルトニアンとして，
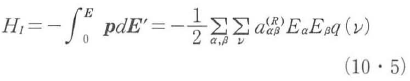
と書ける6)．以下で，この式をもとに古典論を量子論に変換する．
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。