28・5・1 超高速分光-1

[1] 半導体における超高速分光

原子・イオンや分子を対象として発達してきたレーザー分光法は固体やのイオン，さらに半導体や半導体量子構造について応用されるという進歩をとげた．

2準位系の光学遷移に対して開発されてきた飽和分光，コヒーレント分光(自由誘導減衰，フォトンエコー)，量子ビートなどは半導体や半導体量子構造について応用されるが，これは半導体や半導体量子構造が持つ連続的なエネルギー分散を2準位系や2準位系の集合とみなし，対象を連続スペクトルに拡張することに基本がある．

[2] 半導体のポンプ・プローブ分光法

ポンプ・プローブ分光法とは，強いレーザーパルス光により物質の光吸収を過渡的に飽和させ，飽和吸収スペクトルやその時間特性から，物質中の励起状態の動的挙動を探る飽和分光法である．飽和分光法の原理は，不均一に広がった2準位系の光吸収における飽和がホールバーニングを引き起こすと考えて，これを理解するが，固体，特に半導体中のバンド間遷移や励起子生成による吸収スベクトルも，強い入射光により飽和し，ホールバーニングが観測されることがある．バンド間遷移に対応する連続吸収スペクトルは，不均一広がりと呼ぶことはできないが，位相緩和で広がった均一広がりでもない．半導体中の電子には波数kの自由度があり，波数kとエネルギーEの間の関係(分散関係)が連続吸収スペクトルを生み出す．半導体中のバンド間遷移が飽和する理由は，電子および正孔がフェルミ粒子なので，パウリの原理により，占有された状態を新たに励起できないからである．

図28・24に示すようなバンド間選移による連続吸収スペクトルの飽和を，吸収スペクトルの変化分を吸収スペクトルで規格化した-Δα(E)/α(E)で表すと，

と書くことができる．ここで，f_e(E_e)，f_h(E_h)は，エネルギーE_eおよびE_hを持つ電子・正孔の分布関数，Eは測定する光子エネルギーでもある．もしも，電子や正孔が格子と熱平衡に達しているならば，電子や正孔は格子混度でのフェルミ分布で表されるが，過渡的には電子・正孔は格子と熱平衡の分布にはない．エネルギーギャップをE_g，電子・正孔の有効質量をそれぞれm_e，m_h，換算質量をμ=1/(1/m_e+1/m_h)で表し，伝導帯，価電子帯の分散関係に基づいて，図に示すような垂直遷移を考えると，EとE_e，E_hとの間には，

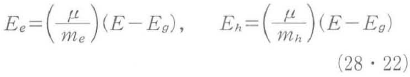
の関係が導ける．

式(28・20)，(28・21)からわかるように，吸収スペクトルの変化分を検出すれば，半導体中に励起された電子・正孔のエネルギー分布を知ることができる．フェムト秒(10^-15 s)域の超短パルスレーザー光で半導体中に電子・正孔をバンド間励起し，吸収スペクトルの変化を刻々と調べると，電子・正孔のエネルギー分布の時間変化を直接追跡することができる．

フェムト秒光パルスを用いることにより，物質中での励起状態の動的様相をフェムト秒の時間尺度で探る光物性研究が可能になる．5 fsの時間幅の光パルスは，不確定性関係から約0.13 eVのスペクトル幅を持ち，時間が短いほどスペクトル上からの情報としては貧弱になるので，研究の必要に応じて，超短パルスあるいはスペクトル的にもある程度狭められた光パルスを用いたポンプ・プロープ実験が行われる．高い時間分解能を持つポンプ・プローブ法でスペクトル情報を得る方法として，超短パルス幅を持つ白色光の利用がある．超短パルス白色光は，尖頭出力0.1 GW程度まで増幅された強い超短パルスレーザー光を水，エチレングリコール，石英ガラス，サファイアなどに集光させることで得られる．白色光の一部はフィルタなどを用いてスペクトル的に一部を切り取り，励起光(ポンプ光)に用いたり，プローブ光に用いたりする．ポンプ光に対し，プローブ光を時間的に遅延させて，吸収の時間的変化として測定する．ポンプ・プローブ法によれば，光検出器の時間分解能に左右されず，レーザーのパルス幅によって決定される分光が可能であるが時間分解能は，不確定性原理により光検出のスペクトル幅には左右される¹³³⁾．実際，フェムト秒域の超高速ポンプ・プローブ分光法は，以下にも述べるように，半導体量子構造にさかんに応用されている^134)135)．

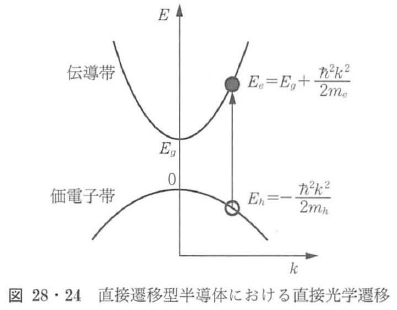
白色光を用いたポンプ・プローブ測定の一例として，量子ドット中の反結合2励起子状態が発見された例を図28・25に示す．この例は時間分解能よりはスペクトル分解能が優先された場合で，サイズ分布などで不均一に広がったCuCl量子ドットの励起子吸収スペクトル中をフェムト秒パルスからスペクトル的に切り出されたピコ秒ポンプ光でサイズ選択励起をおこなうと，ポンプ・プローブスペクトルに，量子ドット中の反結合2励起子状態に起因する誘導吸収が見られる¹³⁶⁾．誘導吸収帯の時間変化は励起子寿命を反映している．この反結合2励起子状態は3次元的な量子閉じ込めの起こる量子ドットに特有の状態であり，量子ドットの光学非線形性に重要な寄与があると考えられている．

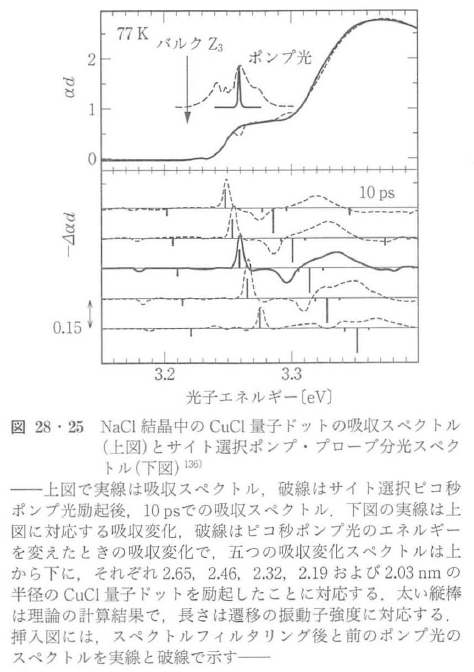
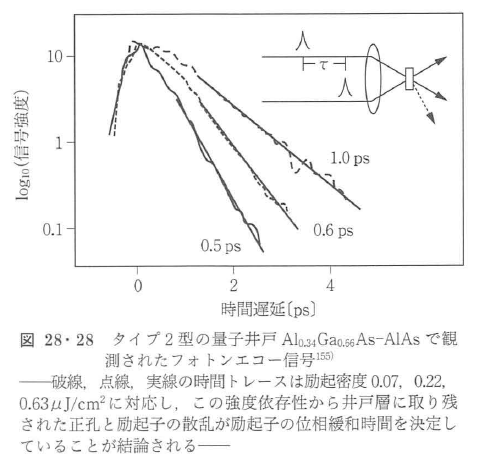
電子と正孔の分布の総和がポンプ・プローブ分光法で検出されるが，空間的に電子と正孔が分離する場合には，ポンプ・プローブ信号にそれぞれが分離して現れてくる．タイプ2型の量子井戸Al_0.34Ga_0.66As-AlAsでは，光励起されてAl_0.34Ga_0.66As量子井戸中に生成された電子・正孔対は，井戸層と障壁層にある電子の波動関数の混じり合いを通じて，電子が井戸層から障壁層へトンネルし，井戸層には正孔だけが取り残され，ポンプ直後には電子・正孔両者の分布，電子・正孔の空間分離後は正孔の分布がポンプ・プローブ信号に現れる．このようすが，白色光を用いたポンプ・プローブスペクトル¹³⁷⁾にも，図28・26に示す1ビームを用いたポンプ・プロープ時間トレース¹³⁸⁾にも，明確に観測される．

80 MHz程度の高繰返しモード同期チタンサファイアレーザーを用いた1ビームポンプ・プローブの場合，プローブ信号中のポンプによる変化分にして10^-8の信号を測定するのはむずかしくない．これは，アルゴンレーザー励起のモード同期チタンサファイアレーザーのパルス強度ゆらぎが2％以下(レーザーダイオード励起の固体グリーンレーザー励起の場合:0.1％以下)のうえ，約80 MHzの高い繰返しを持ち，それより低い周波数のさまざまな変調手法が使えることが大きい．高感度ポンプ・プローブ法を用いて，電子遷移の飽和分光だけでなく，格子振動をとらえるコヒーレントフォノンの分光も盛んにおこなわれている．結晶中の格子振動は振動数の高い光学型フォノンでも20~40 meV(4.8~9.7 THz)，振動周期にして100~200 fsの時間領域にあり，フェムト秒の時間分解能で計測できる．格子振動は物質の屈折率・誘電率を変化させるので光反射や光透過強度の時間的変化としてポンプ・プローブ法により検出される．微小信号を測定する必要性から1ビームポンプ・プローブ法を変調分光と組み合わせて用いることが多い．

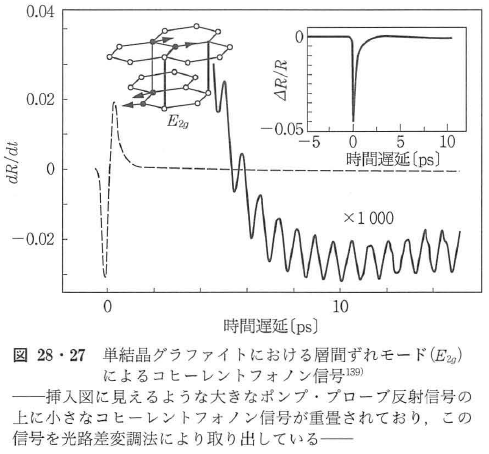
変化分にして10^-8のポンプ・プローブ信号が測定された見本としては，図28・27に示すような単結晶グラファイトからのコヒーレントフォノンの測定があげられる¹³⁹⁾．この測定では，試料に加えるポンプ光とプローブ光の到達時間差に変調を加えて熱的な効果を一定にし，2個のバランスされたフォトダイオードでわずかなレーザー光強度の変動を相殺した測定になっている．コヒーレントフォノンの測定対象としては，有機結品^140)141)，半導体結晶¹⁴²⁾，半導体超格子^143)144)，超伝導体¹⁴²⁾，層状結晶^142)145)，半金属¹⁴²⁾，量子ドット^146)147)などがある．コヒーレントフォノンに起因する時間トレースが2成分以上の振動成分を持っている場合，時間トレースの振動信号をフーリエ変換してスペクトル信号にする解析が成功している例は多い¹⁴⁸⁾．たとえばGaAs-AlAs超格子のゾーン折り返しモードの二重項が明確に観測されている^143)144)．

[3] 半導体のフォトンエコー

固体中の電子選移は均一広がりと不均一広がりを持っている．不均一広がりの幅が均一広がりより広くて光吸収スペクトルを支配している場合，光吸収スペクトルで測定できるのは不均一広がりである．均一広がりは遷移双極子の位相が相互にランダム化する時間(横緩和時間または位相緩和時間(T₂))の逆数で決まり，準位の寿命(縦緩和時間(T₁))の逆数で決まる寿命広がりを含む．縦緩和時間は，発光寿命を測定すれば決めることができる．一方，横(位相)緩和時間を測定する方法がフォトンエコーである．他方，均一幅あるいは，横(位相)緩和時間をスペクトル領域から非線形分光法を用いて測定するのがホールバーニング分光である．

第一の光パルスが不均一に広がった周波数を持つ光遷移双極子を初期位相をそろえて励起し，それらが位相緩和時間T₂で緩和したあと，第二の光パルスを時刻t₁₂に加えると，不均一広がりにより時間的に位相がばらばらになった遷移双極子を時間反転することで第二光パルスの照射のあとt₁₂の時間を経て位相がそろい，巨視的電気分極が発生してフォトンエコーが発生する．このとき，電気分極は位相緩和を受けていない遷移双極子の大きさに比例するので，t₁₂を大きくするときフォトンエコーの大きさの減衰時間が遷移双極子の位相緩和時間，不均一広がりの影響を受けない分極の位相緩和を直接に表すことになる．フォトンエコーの強度は，不均一幅が均一幅にくらべて十分大きい場合，exp(-4t₁₂/T₂)に比例している¹⁴⁹⁾．横緩和時間T₂が求められると，幅(半値全幅)はΓ_h=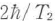で与えられる．

フォトンエコー法が半導体の励起子系について初めて用いられたのは，励起子ポラリトンの位相緩和が調べられた時間分解非縮退4光波混合₁₅₀₎で，そのあと，時間分解縮退4光波混合により量子井戸中の励起子の位相緩和¹⁵¹⁾，バルク半導体中の電子の位相緩和¹⁵²⁾，量子ドット中の励起子の位相緩和^153)154)が，フォトンエコー法により詳しく調べられた．図28・28に，タイプ2型の量子井戸Al_0.34Ga_0.66As-AlAsで観測された，井戸層に取り残された正孔と励起子の散乱が励起子の位相緩和時間を決定した例を示す¹⁵⁵⁾．

一方，励起状態の寿命がレーザーの繰返しの時間間隔より長いと，蓄積フォトンエコーの測定が可能となる^156)157)．蓄積フォトンエコーの長所は繰返し光パルスによる蓄積効果のために，微弱光を用いてもフォトンエコー信号をとらえることができることで，フォトンエコーでしばしば問題になる励起キャリヤ間の衝突による位相緩和がまったく問題にならない強度でのフォトンエコー測定が可能である点にある．

フォトンエコーの測定には，励起光，エコー信号光の聞に位相整合条件が満足される必要がある．3本の励起光の波数をk₁，k₂，k₃エコーパルスの波数をk_eとすると，蓄積フォトンエコー測定では，図28・29に示すように，同軸でない配置(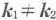，k₃=k₁)でエコーの観測方向としてk_e=k₂の条件はしばしば用いられる．この場合，エコーパルスk_eはプローブパルスk₂と干渉することになる．プローブパルスk_eの電場とこれにくらべてずっと弱いエコーパルスk_eの電場の和の2乗に比例する光強度を受ける検出器は，プローブパルスk₂の電場とエコーパルスk_eの電場の積に比例し，エコー強度はexp(-2t₁₂/T₂)に比例して減衰する¹⁵⁶⁾．この指数関数で表される減衰と半値全幅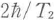を持つローレンツ関数は互いにフーリエ変換の関係にあり，位相緩和時間T₂から均一幅として半値全幅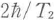が得られる．

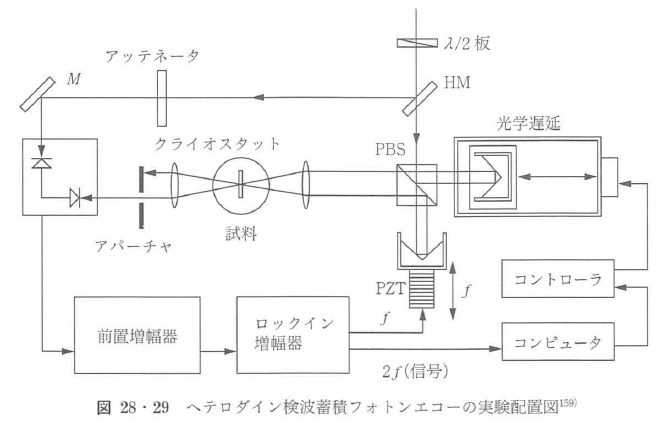
励起光やプローブ光の散乱に隠されやすいエコー信号を感度良く検出するのに用いられる，蓄積フォトンエコー測定で使われた位相変調法による実験配置がある^158)159)．図28・29に示すように，ピコ秒あるいはフェムト秒光パルスをビームスプリッタで二つに分け，それぞれを光学遅延上の反射鏡と圧電素子付きの反射鏡により反射したあとにk₁，k₂の波数をもって試料に集光し，k₂方向からエコー信号を検出する．このとき，k₂は圧電素子により光路長を半波長程度変調しておくと，エコー信号強度もこの周波数で変調されるので，ロックイン増幅器で強度が変調されないk₂から分離されて検出できる．

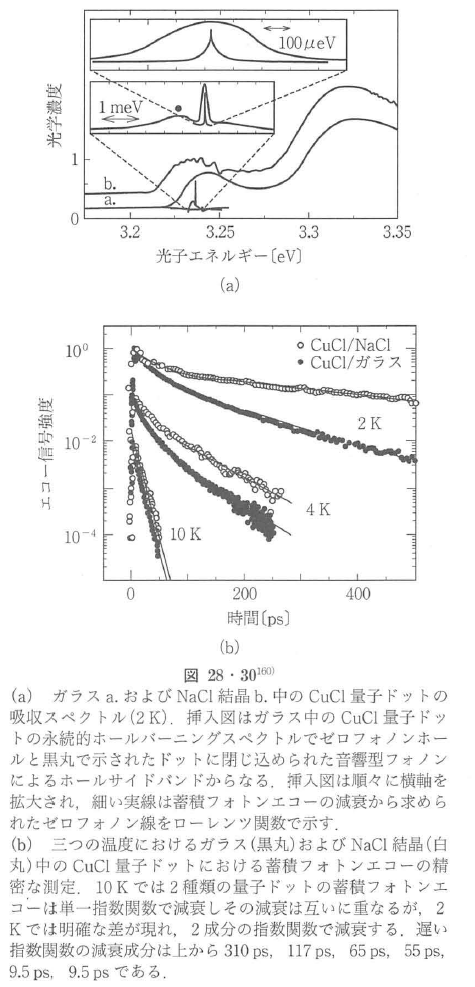
量子ドットにおける蓄積フォトンエコーが弱い閉じ込め量子ドットの典型例であるNaCl結晶およびガラス中のCuCl量子ドットにおいておこなわれている．その測定例を図28・30に示す¹⁶⁰⁾．エコーの減衰は2K，4Kの低温では母体の違いにより異なるが，10 K まで温度が上がると母体によらなくなる．低温では減衰は2成分からなり，速い減衰成分はスペクトル中の幅の広い閉じ込めを受けた音響型フォノンのサイドバンド成分を反映し，遅い減衰成分がゼロフォノン線のスペクトル幅を表す．遅い減衰の時定数の2倍が位相緩和時間T₂を表し，1 KではT₂は1.3 nsにも達する．

[4] 半導体の量子ビート

エネルギーの近い二つの光学遷移が時間の短い光パルスでコヒーレントに励起されると，光励起された二つの分極はわずかに異なるそれぞれ振動数で振動する．これらの光励起された二つの分極は互いに量子干渉し，うなりを生ずる．これが量子ビートである．半導体中の励起子は大きな振動子強度を持っているので，励起子の共鳴発光¹⁶¹⁾，光透過¹⁶²⁾，ポンプ・プローブ¹⁶³⁾，フォトンエコーなどの時間波形に量子ビートが観測される．不均一広がりで発光スペクトルが広がっていても，発光量子準位が微細構造を持ち，その間のコヒーレンスが保たれると，スペクトル領域では不均一広がりで隠されて見えない微細構造が量子干渉し，時間領域で量子ビートとなって観測される．振動の周期Tから光学遷移間の微細なエネルギー差h/Tが測定される．

固体中の励起子の量子ビート，自由誘導減衰の実験の好例としてZnP₂単結晶の励起子に関しての研究がある¹⁶⁴⁾．この結晶は弱い吸収を持つ励起子のシリーズが高次まで見え，図28・31に示すように，このn=1の励起子にフェムト秒パルスを合わせて透過したパルスの時間トレースを第二高調波による時間ゲートにより計測すると，n=1の励起子の自由誘導減衰，ポラリトンビート，コヒーレントディップが観測される．コヒーレントディップが見えるのは，光により作られた励起子の双極子と光波が互いに干渉するからである．また，ポラリトンビートは上枝と下枝のポラリトンが伝搬しながら同じ群速度で走る部分どうしの干渉である¹⁶²⁾．n=2,3,4励起子にフェムト秒パルスを合わせて透過したパルスの時間トレースは，自由誘導減衰のすそに励起子間の量子ビートが観測された．

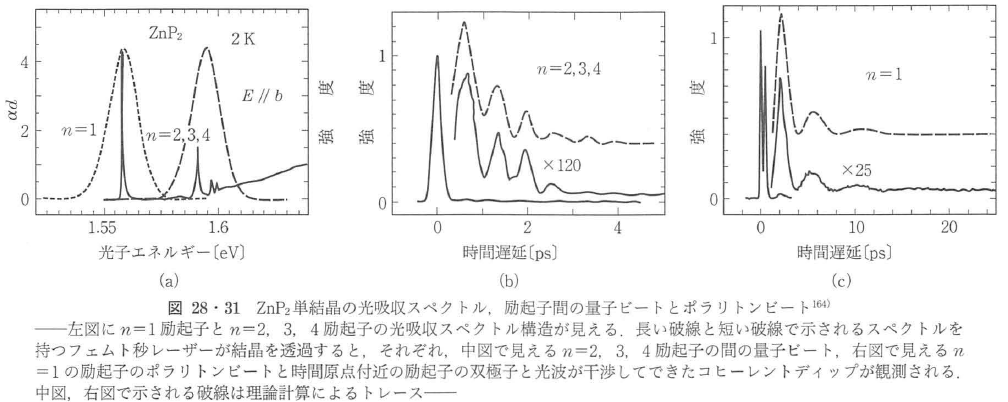
量子ビートは振動の周期Tと光学遷移間の微細なエネルギー差h/Tが逆数の関係で結び付いているので，きわめて小さなエネルギー差は周期としては長く，スペクトル微細構造を時間領域で調べる優位性がある．この優位性に注目して量子ビートを用いて，磁場下で量子井戸^162)165)166)や量子ドット^167)168)のスピンに依存した微細構造を調べるのにも利用できる．

28・5・2 超高速分光-2