レーザーからは従来光源では得られない強い光電場が発生される．物質は主に光電場により生成される電気分極を介して光波と相互作用する．強い光電場照射下の非線形電気分極から生じるさまざまな効果を扱うのが非線形光学である．

本章では，非線形光学効果全般を解説し，非線形光学素子に用いられている材料を概説する．

7・1・1 非線形分極

光波に応答する微視的な電気双極子の集合体が電気分極Pである．この物質の非線形光学応答を効果の大きい順に並べると，電気分極ベクトルPの各成分Piを電場あるいは光電場Eの各成分Eiにより展開して次式のように表される．

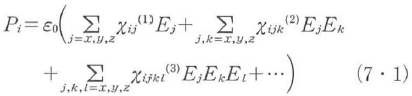
ε₀は真空中の誘電率，χ_ij⁽¹⁾，χ_ijk⁽²⁾，χ_ijl⁽³⁾は2，3，4階のテンソルで表される1，2，3次の電気感受率である．

式(7・1)において，第2項以下が非線形分極である．

第1項は大きさのみを考えると，分極が電場に比例する線形分極である．その係数である1次の電気感受率がテンソルで表されているのは，物質が電場に対して異方性のある応答を示すことを意味する．たとえばP_x=ε₀χ_ij⁽¹⁾E_yはy方向への電場印加あるいはU偏光入射に対してx方向の分極が生じることを意味する．これより，異方性材料においては，互いに直交する二つの偏光に対して異なる二つの屈折率がある複屈折性が生じる．複屈折性は，波長変換における位相整合で利用される(後述)．

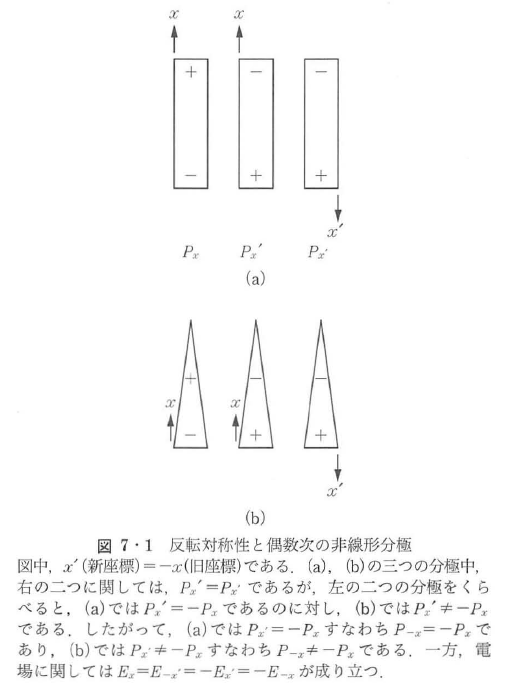
第2，3項が電場の2，3乗に比例する分極，2，3次の非線形分極を表す．第2項，一般に偶数次の非線形分極は，反転対称性を欠く物質にのみ現れる．「反転」は座標を反転することで，たとえば1次元で考えると，-xをZ で置き換えて物理量を見ることを意味する．

図7・1¹⁾において-x→xとすると一般に，電場は物質と無関係な「場」であるので，つねにE_-x = -E_xである一方，「分極を見る」ことは「物質の形を見る」ことであるので，図(a)のように反転対称性がある場合はP_-x = -P_xである．このとき，P_-x = ε₀χ_xxx⁽²⁾E_-xE_-x = ε₀χ_xxx⁽²⁾E_xE_xに対して-P_-x = -ε₀χ_xxx⁽²⁾E_xE_xであるので結局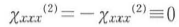，となり，2次の非線形分極は生じない．図(b)のように反転対称性がなければ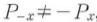， したがって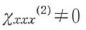である．-x→xという反転操作はUまたはz軸の周りに半回転させることを意味するが，このとき反転対称性がなければx方向の偶数次の非線形分極が生じる．

式(7・1)においてP_i(r，t)，E_j，k，lは空間rおよび時間tに依存する．マクスウェル方程式やこれから導びかれる非線形波動方程式においては，分極や電場は式(7・1)の形で扱われる．ただし，関与する光波の周波数とその電場により誘起される分極の周波数との関連や電場の積E_jE_k，E_jE_kE_lの順序の交換を明確にする場合には，以下のように表される．

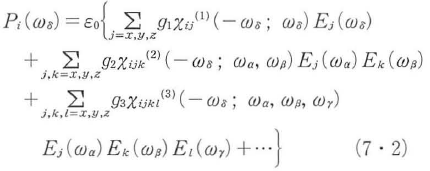
ω_{α，β，γ，δ}は関与する光放の角周波数であるが，静電場のときは0とすればよい．縮重度g_1，2，3は，式(7・1)の非線形分極から生じる種々の非線形光学効果に応じてさまざまな値をとる．以下，特別に断らない限り，和はx，y，zについてとることを意味する．

式(7・1)，(7・2)において，第1，2，3，・・・項間の和をとることは，各項の周波数依存性が異なる場合には意味を持たず，各項ごとに独立に考える必要がある．

式(7・2)は時間・空間に依存する角周波数ω，波数kの分極および電場を，

と表したときのP(ω)とE(ω)の間の関係である．式(7・1)，(7・3)式から得られる式(7・2)の縮重度については後述する．ただし，容易にわかるように，g₁=1である．

7・1・2 非線形光学効果