本章では，非線形光学効果を用いたさまざまな波長変換について解説する．レーザー光の波長あるいは周波数を変換して得られる光波は，レーザー光と同等のコヒーレンスを有する．

8・1・1 非線形分極波とマクスウェル方程式

非線形分極が効果を発現するのは，強い光電場のもとである．レーザー光は通常光源とくらべると，単色性，指向性，空間的干渉性などの諸点において桁違いに優れている．これらの特長が相からまってレーザー光は，非線形光学効果を顕著にするうえで十分な強電場を容易に提供してくれる．各種非線形光学効果のうちで有用なものの一つが，非線形光学媒質からの新たなコヒーレント光の発生，レーザー光の波長変換である．

式(7・1)第2，3項の巨視的な非線形分極から生じる新たな光波のふるまいは，非線形マクスウェル方程式から導かれる波動方程式を用いて論じることができる．いま，2次あるいは3次の非線形分極を一般にP_NL，これから生じる光波の電場をEと置くと，

が右辺に強制振動の項P_NLを含む非線形波動方程式である．式(8・1)において，μ₀，εは真空の透過率，媒質の誘電率である．媒質は非磁性とした．式(8・1)は，入射したレーザー光により媒質中に非線形分極が生じる過程については触れていないが，非線形分極が新たな光波の発生源となるようすを強制振動P_NLによって光電場Eが生じる過程として表している．

簡単のため，非線形分極波P_NLはz方向に伝搬し，その角周波数，波数をそれぞれω_NL，k_NL，振幅を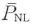とすると，

で表される．式(8・2)は位相速度ω_NL/k_NLで伝搬する波で，式(8・1)において強制振動を与える項となる．その斉次解である角周波数ω_NL，波数k(ω_NL)の光電場Eの振幅が強制振動のため，Z方向に伝搬するにつれて変化するという定数変化法に従って式(8・1)を解くことができる．

光電場を，

と置き，式(8・2)とともに式(8・1)に代入して，E(z)を求める．{k(ω_NL)}²=ω_NL²μ₀(ω_NL)を用いると，

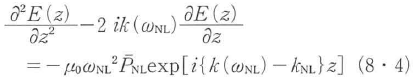
が得られる．ここで，波長程度の伝搬長では振幅の増加分は変化しない．すなわち，

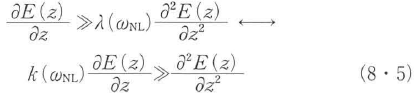
を仮定(SVEA)すると，式(8・4)は，

に帰着する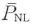．のz依存性がない場合には，式(8・6)は容易に積分でき，非線形媒質の長さをLとすると，

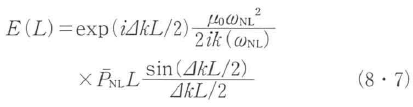
が得られる．ここで，

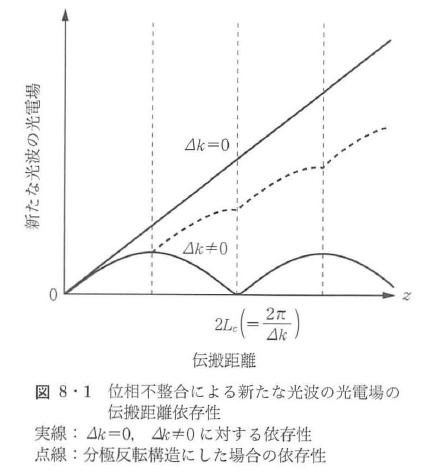
は，非線形分極波の波数k_NLと新たに生じた光波の波数k(ω_NL)の不一致，言い換えると位相速度の不一致を表す．非線形分極波と新たな光波の位相速度が一致すると，伝搬する非線形分極波から生じつづける新たな光波は可干渉に重ね合わせられ，その振幅は各点で発生される光波の振幅の和となるので，伝搬長に比例して増大する．Δk=0と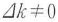の場合の|sin(Δkz/2)|を示したのが図8・1の実線である．Δk=0とすることを位相整合をとるという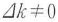．の場合，正の重ね合せが起こっている最初のピークまでの長さ，Δkz/2=π/2に対応するLc=π/Δkを実効コヒーレンス長という．これはレーザー光のコヒーレンス長とは異なる定義の量である．

生じた光波の強度Iの媒質長L依存性は，

で与えられる．Δk=0の場合は，式(8・9)右辺はL²である一方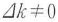，の場合，その最大値は(2L_c/π)²である．可視波長領域近辺の波長変換におけるコヒーレンス長は数μm前後から数十μmにすぎないことを考えると，位相整合をとることは，効率の良い波長変換にとって必要不可欠の条件である．

ここで，7章で詳説した種々の波長変換とω_NL，k_NL，k(ω_NL)との対応を見ておく．

「3光波混合と光第二高調波発生」においては，ω_NL=ω₁±ω₂，k_NL=k(ω₁)±k(ω₂)，k(ω_NL)=k(ω₁±ω₂)として，微分方程式(8・6)，したがってその解(8・7)式はそのまま使用することができる．