媒質を連続体と考えれば、マックスウェルの方程式から、
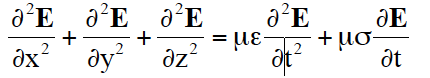
(式1)
を得る。右辺の第2 項は、振動子モデルの減衰項に相当する。電界の時間変化によって交流電流が流れる。媒質は抵抗性であるから、光は熱エネルギーに転化される。
誘電率(従って屈折率)を複素量として再定義すれば、減衰を受けない波動方程式と同じ形にこの式を書き換えることができる。複素屈折率
![]()
(式2)
を非導電性媒質の場合の解に代入するだけでよい。式2で、nR・nIは共に実数である。y 方向に伝搬する平面波の電界は
![]()
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
