式1の総和は、複素平面上のベクトル加算として図示できる。電気工学分野では複素振幅は位相子として知られる。大きさと位相を使ってE0∠αと略記することがある。
![]()
で示される波動を考える。図1a には、角速度ωで反時計方向に回転する長さE01のベクトルを描いている。垂直軸への射影がE01sin(ωt + α1)となる。余弦波の場合は水平軸への射影を考えればよい。回転ベクトルが位相子 E01∠α1である。R・I は各々、実軸・虚軸を示す。
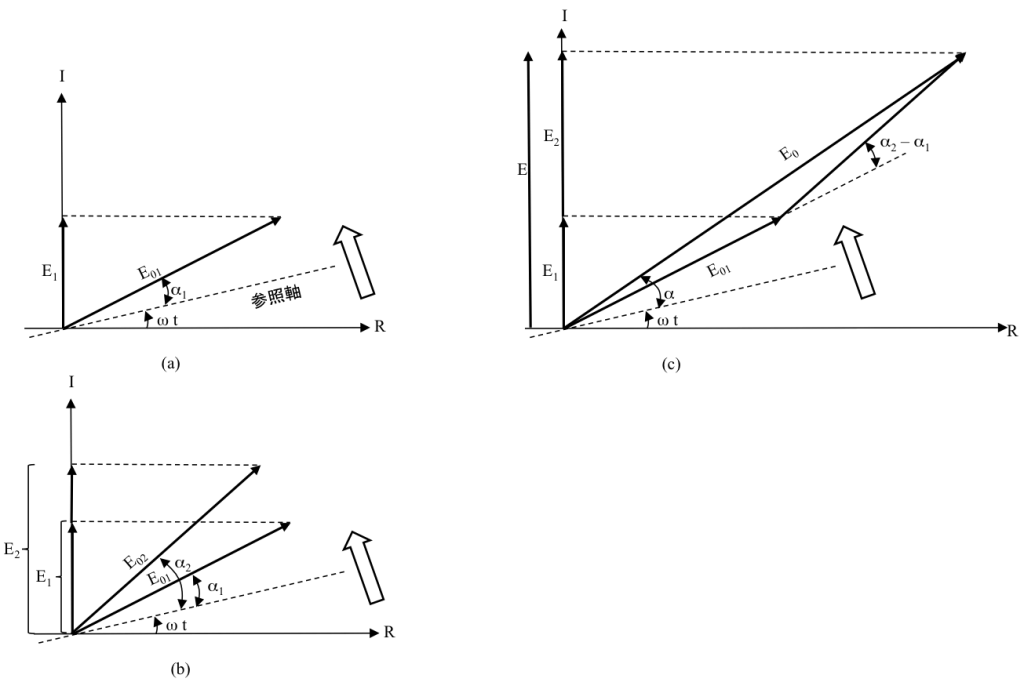
図 1 位相子の加算
第2 の波動
![]()
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
