対象領域の空気量が増加した場合を考える。例えば、体積がλ3の標準気圧空気の立方体領域には、約300万個の分子が存在する。近接している(≈3nm)散乱体からの2次波の相互位相はランダムとはならず、干渉が重要になる。前方方向では強め合う干渉となるが、それ以外の方向では弱めあう干渉が優勢となる。高密度媒質中では、横方向・後方への散乱光は全く存在しないか、あっても極めて少ない。下記図は、規則正しく格子状に配置された散乱体中を光ビームが伝搬する様子を示す。
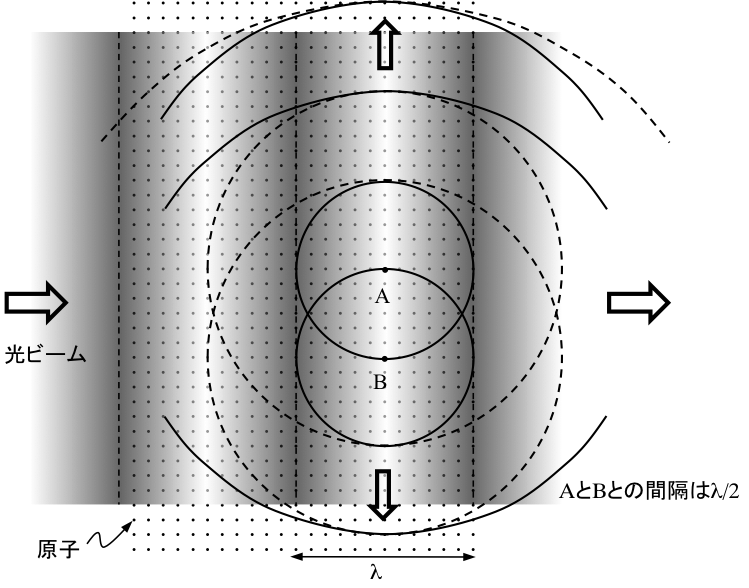
図 高稠密媒質による横方向散乱 原子が密に並んだ媒質へ、左から平面波が入射する。
(十分密なために、)任意の原子Aに対して半波長だけ離れた原子Bが存在する。
両原子が放射する2次波は弱め合う干渉をする。ビームに直交する方向では完全に打ち消し合う。
ある分子Aは球面状に光を散乱する。格子間隔はλに比較して十分稠密であるから、同一入射波面上でAから約λ/2だけ離れた分子Bが必ず存在する。A・Bからの横方向散乱波は互いに打ち消し合う。散乱体の稠密さを考慮すると、任意の横方向において、2次波が互いに打ち消し合う分子対が常に存在するであろう。
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
