透過と屈折率

屈折率(n=c/v)が1と異なる均質媒質を透過する光ビームの位相速度は、真空中の光速cではない。しかし、光子の速度cに変わりはない。

どうして、このようなことが生じるのか？各原子で散乱された波は、前方方向でのみ同位相で重なり合い2次波を構成する。入射波である1次波も2次波もともに、原子間の空間を速度cで伝搬するにもかかわらず、両者が重なりあって形成される透過波の位相速度は、cよりも小さいときも大きいときもある。この矛盾を解くカギは、１次・２次両波の位相関係にある。

散乱原子・分子をモデル化した電子振動子の位相は、低周波数で駆動力(1次波)と同相である。周波数が大きくなると振動子位相には遅れが生じ、周波数増にしたがって位相遅れも増大する。周波数が共振周波数に至ると振動子位相は90°遅れとなる。さらに周波数を大きくすると、十分高周波では180°遅れとなる(下記図b)。2次波の位相は振動子に対して90°遅れるので、1次波に対する2次波の位相は、低周波で90°～180°の遅れ、共振周波数以上で180°～270°遅れ(↔90°～180°進み)となる (下記図参照)

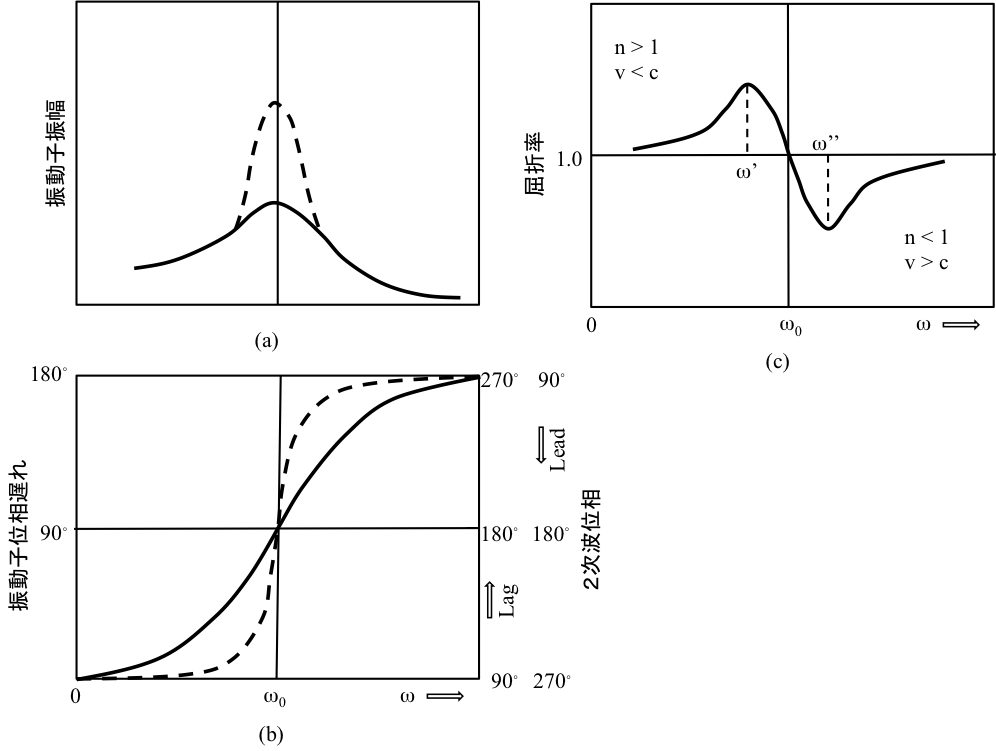
図　減衰振動子の駆動周波数依存性 (a) 振幅 (b) 位相遅れ (c) 屈折率