英国の物理学者ストークス(Sir George Gabriel Stokes, 1819-1903)は、境界面での反射・透過現象に対して、より優雅で斬新な見方を展開した。振幅E0iの入射波が入射角θ1で境界面に入射している(図(a))。
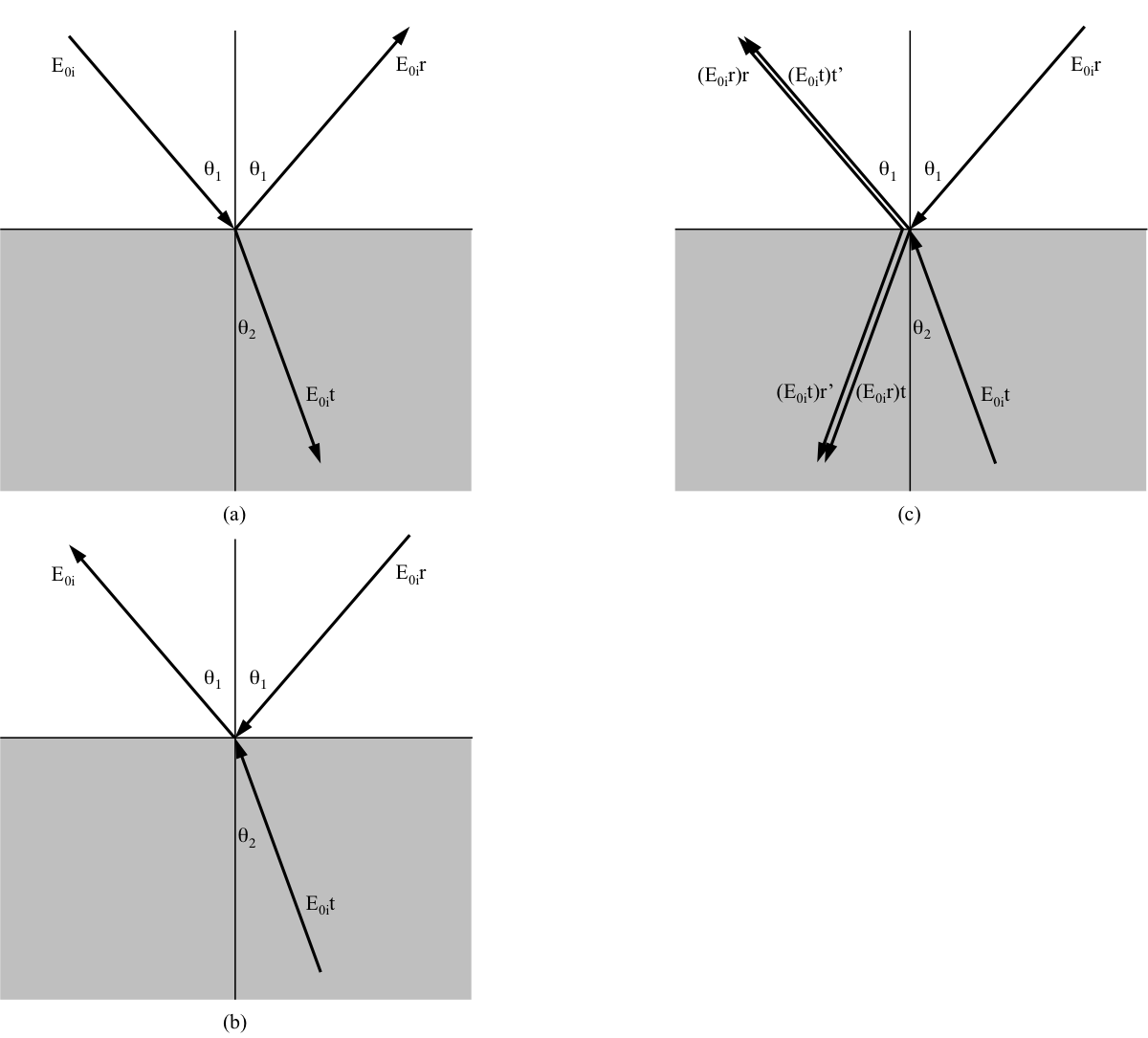
図 ストークスの取り扱いによる反射と屈折
透過角はθ2、反射波・透過波の振幅は各々 r E0id・t E0iである。ここでr・t は振幅反射係数・振幅透過係数である。エネルギーの散逸(吸収)はないと仮定すると、波動の進行は可逆的であるから、図(b)の状況は物理的にあり得る。振幅がr E0iとt E0iの波が境界面に入射し、振幅E0iの波が境界面から離れていく。全ての想定される反射波・透過波を示すと上記図(c)のようになる。入射波 r E0iに対応する反射波・
透過波の振幅はr r E0i・t r E0iである。また、入射波 t E0iに対応する反射波・透過波の振幅を r’ t E0i・t’ t E0iとする。
図(c)が図(b)と等しくなることから、
![]()
(式1)
![]()
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
