理想的な点光源を考える。波面は、光源位置を中心とする同心球状に周囲空間へ広がっていく。波面がもつ対称性から、極座標で記述することが便利であると考えられる。極座標系でラプラス演算子は、
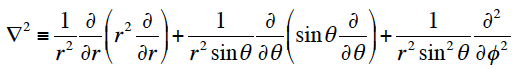
で与えられる。ここで、r, θ, φは次式で定義される。
![]()
球対称な波動はθ, φには依存しないので、球面波ψ(r)は、
![]()
とおくことが出来る。ψ(r)にラプラス演算子を作用させると、
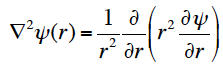
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
