電磁波が物質表面に入射すると、物質を構成する電荷と相互作用する。吸収・反射いずれの場合も、電磁波は電荷に力を及ぼし、結局、物質に力が働く。
前記の力は電磁論によって計算することができる。さらに、ニュートンの第2法則(力は運動量の時間変化率に等しい)から、電磁波が運動量を伴うことが示唆される。実際、エネルギー流には常に運動量が付随すると考えることは合理的である。
マクスウェルが示したように、放射圧Pは電磁波のエネルギー密度に等しくなる。電界エネルギー密度uEと磁界エネルギー密度uBは、ポインティングベクトルの導出に用いたように、
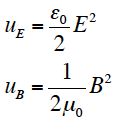
P = u = uE + uB であるから、
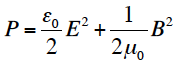
放射圧Pはポインティングベクトルの大きさSで表すことができて、
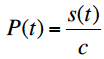 …式1
…式1
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
