複素平面原点と複素指数波動関数値とを結ぶ矢印を位相子と呼ぶ。振幅A、位相φの位相子をA∠φと記す。
二つの調和波ψ1, ψ2の重ね合わせとなる合成波ψについて位相子を用いて考える。ψ1, ψ 2, ψの振幅をA1, A2, A、相対位相をφ1, φ2, φとする。合成波を示す位相子A∠φは、位相子A1∠φ1, A2∠φ2を複素平面上で(複素ベクトルとして)加えることで得ることができる
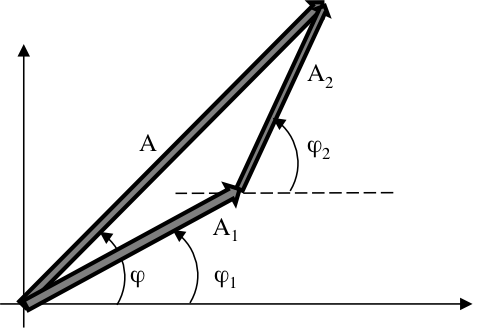
図 要素波の位相子をベクトル加算することで合成波の位相子を得ることが出来る。
参考文献
無料ユーザー登録
続きを読むにはユーザー登録が必要です。
登録することで3000以上ある記事全てを無料でご覧頂けます。
登録することで3000以上ある記事全てを無料でご覧頂けます。
- @optipedia.info ドメインより登録の手続きを行うためのメールをお送りします。受信拒否設定をされている場合は、あらかじめ解除をお願いします。
- Gmailをお使いの方でメールが届かない場合は、Google Drive、Gmail、Googleフォトで保存容量が上限に達しているとメールの受信ができなくなります。空き容量をご確認ください。
